著者：JAXA宇宙科学研究所尾崎直哉

高校数学・物理で学ぶスイングバイ軌道の作り方①
〜軌道伝播をしてみよう〜

スイングバイとは｜ Pythonプログラミングの事前準備｜太陽の周りを回る地球の軌道
漸化式から微分方程式へ｜まとめ

この記事では、高校数学・物理の知識とPythonプログラミングに関する入門的な知識から、”スイングバイ”を活用した軌道設計を行うまでのプロセスを丁寧に説明し、読者に実際に計算してもらうことを目的として書かれている。軌道設計とは、人工衛星や探査機が飛行するルートを計画することである。旅行の計画を立てる際に、移動ルートを真っ先に考えなければいけないように、宇宙ミッションを考える際に、真っ先に考えなければいけないことが軌道設計である。しかし、厄介なことに、軌道設計には数学•物理•プログラミングに関する基礎知識と、軌道力学•最適化に関する専門知識が必要である。このような知識がなければ、移動ルートすら決められないのが、いまの宇宙ミッションなのである。そこで、この記事では、高校数学•物理の知識から出発し、この記事を読み終えた頃には、「はやぶさ」のような探査機の軌道設計ができる一歩手前まで到達してもらいたいと考えている。

同時に、この軌道設計を通じて、高校数学・物理を勉強することが実用的にも役に立つと感じていただければ幸いである。米宇宙開発の父と呼ばれるフォンブラウンも、数学が苦手だったらしいが、宇宙に魅せられて必死に勉強するようになったと言われている。この記事が読者にとって、数学•物理•プログラミングを学ぶモチベーションに繋がれば幸いである。

スイングバイとは

さて、本記事のメイントピックであるスイングバイ(Swing-by)について、簡単に解説しておきたい。スイングバイとは、天体の運動と重力を利用して、探査機の速度ベクトルを操作する軌道設計のワザである。全く同じ意味で、重力アシスト(Gravity Assist)やフライバイ(Flyby)という表現が使われることもある（フライバイは天体の近くを通り過ぎるという意味で、重力で軌道を操作しない場合にも使える一般的な表現である）。ロケットエンジンでは達成できないような速度変化が獲得できるため、スイングバイを活用した軌道設計ができるとドヤ顔ができる。直感的な理解としては、「太陽系」というテニスコートで「地球」が走りながら、テニスラケットで「探査機」というボールを跳ね返すイメージを持ってもらえると概ね正解である。

もう少し正確な解説をしておきたい。まずスイングバイを行うには、太陽・地球等の最低２つの天体と探査機がいる環境が必要である。地球と探査機が太陽の周りを公転していて、探査機が地球に接近する状況を考える。探査機が地球に接近すると、探査機は地球の重力に引き寄せられて、双曲線軌道を描いて軌道が曲げられる。このとき、地球中心の座標系で探査機を観測する（＝地球を原点に固定して、探査機を観測する）と、探査機の軌道はよくある双曲線軌道を描いている。このとき、接近時と離脱時で探査機の速度は変わらないため、何も得していないように思える。

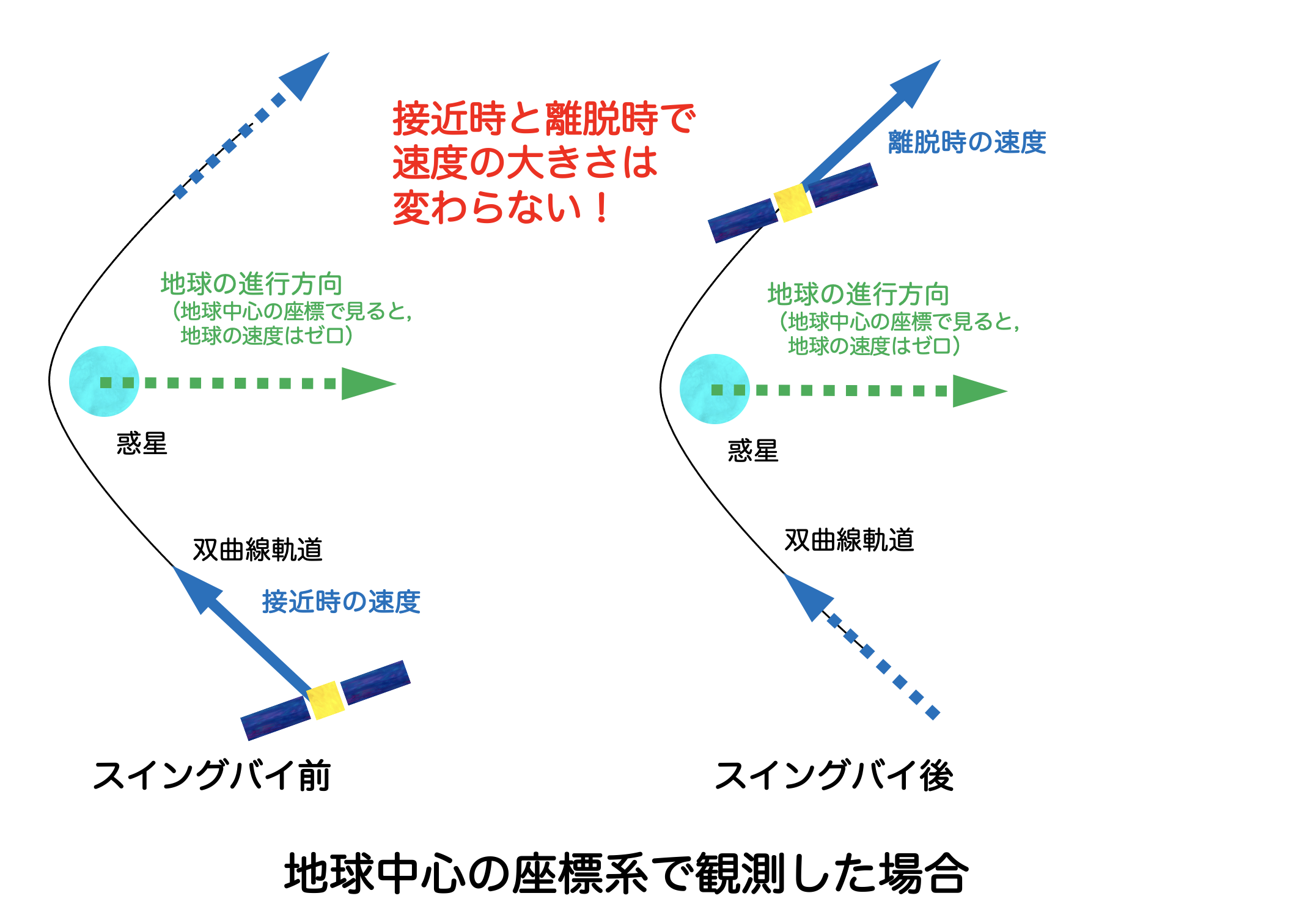
一方、同じ軌道を太陽中心の座標系で観測する（＝太陽を原点に固定し、動いている地球と探査機を観測する）と、どうなるか考えてみよう。太陽中心の座標系では、地球は公転している。そのため、探査機の速度を太陽中心の座標系で考えるためには、地球の公転速度ベクトルの足し算を考えなければいけない。

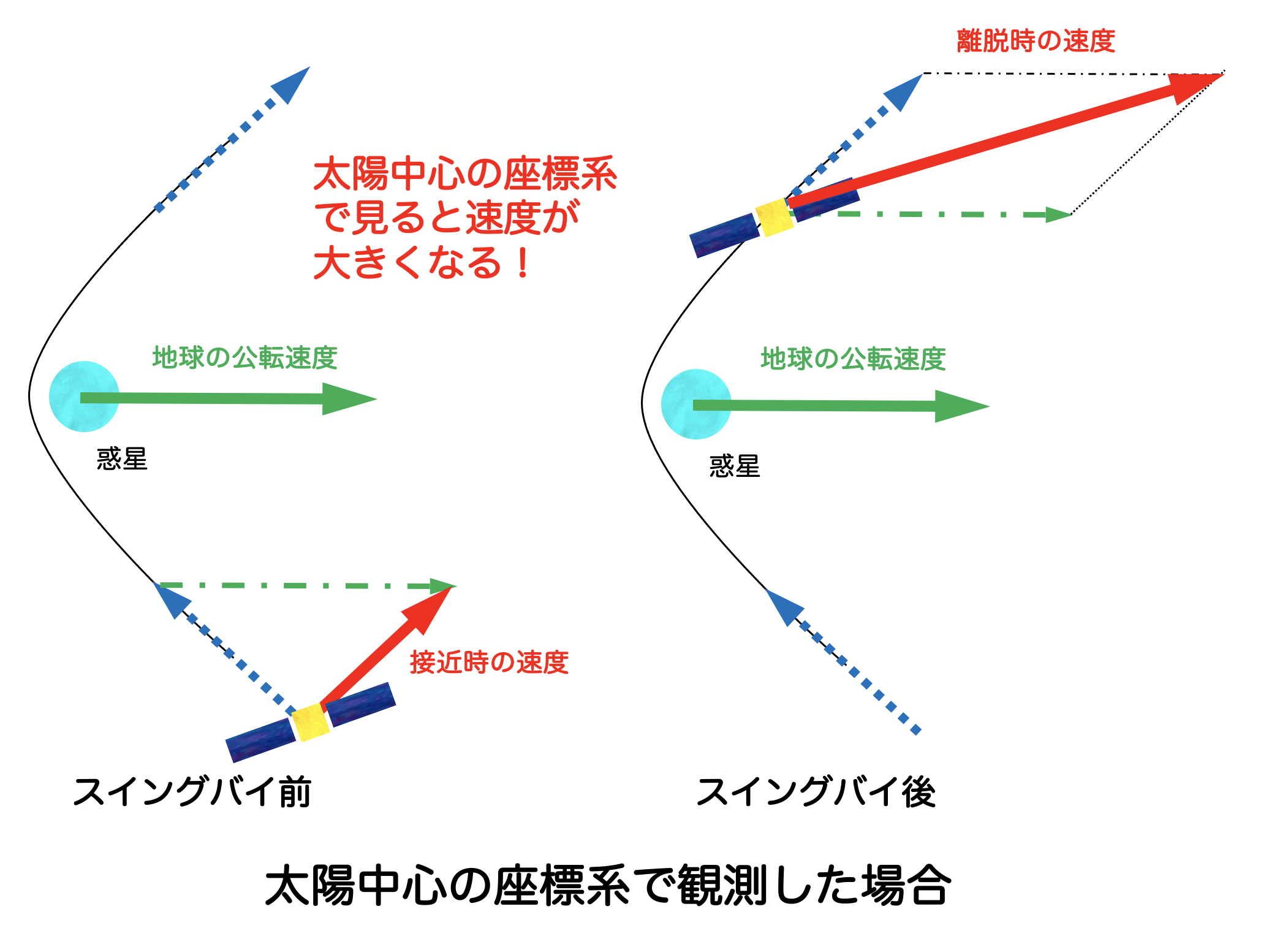
するとどうだろう？地球中心の座標系で観測すると変わらなかったスイングバイ前後の速度の大きさが、太陽中心の座標系で観測すると変わっていることが分かる。この現象が（地球）スイングバイである。上記の説明における、「太陽と地球（地球スイングバイ）」を「地球と月（月スイングバイ）」「太陽と木星（木星スイングバイ）」「土星とタイタン（タイタンスイングバイ）」等に置き換えても成立する。よくある勘違いとして、スイングバイは加速に使うものだと思われることがある。実際は、加速にも使われるし、減速にも使われるし、加速も減速もせずに軌道面を変えるために使われることもある。本質的なことは、スイングバイの対象天体で探査機の速度ベクトルを変えることである。発展的な内容に興味がある読者は、

青のベクトルが大きい/小さい場合に、赤のベクトルの大きさがどのように変わるか？

緑のベクトルの向きや大きさが異なる場合、赤のベクトルがどのように変わるか？

等の考察をしていただきたい。

さて、スイングバイという現象を理解していただけただろうか？本記事の執筆を通じて、筆者自身が改めて「スイングバイを用いた軌道設計」の難易度の高さを実感した。「スイングバイという現象を理解すること」にLv. 1必要だとすると、「スイングバイを用いた軌道設計をすること」にはLv. 50以上必要であると感じている。そのため、多くの一般向け書籍では「スイングバイの現象を解説すること」に留まっている。そのように聞くと、いきなり挫折してしまうかもしれないが・・・本記事では、Lv. 5であっても「スイングバイを用いた軌道設計ができるになる」ように説明したいと思う。

Pythonプログラミングの事前準備

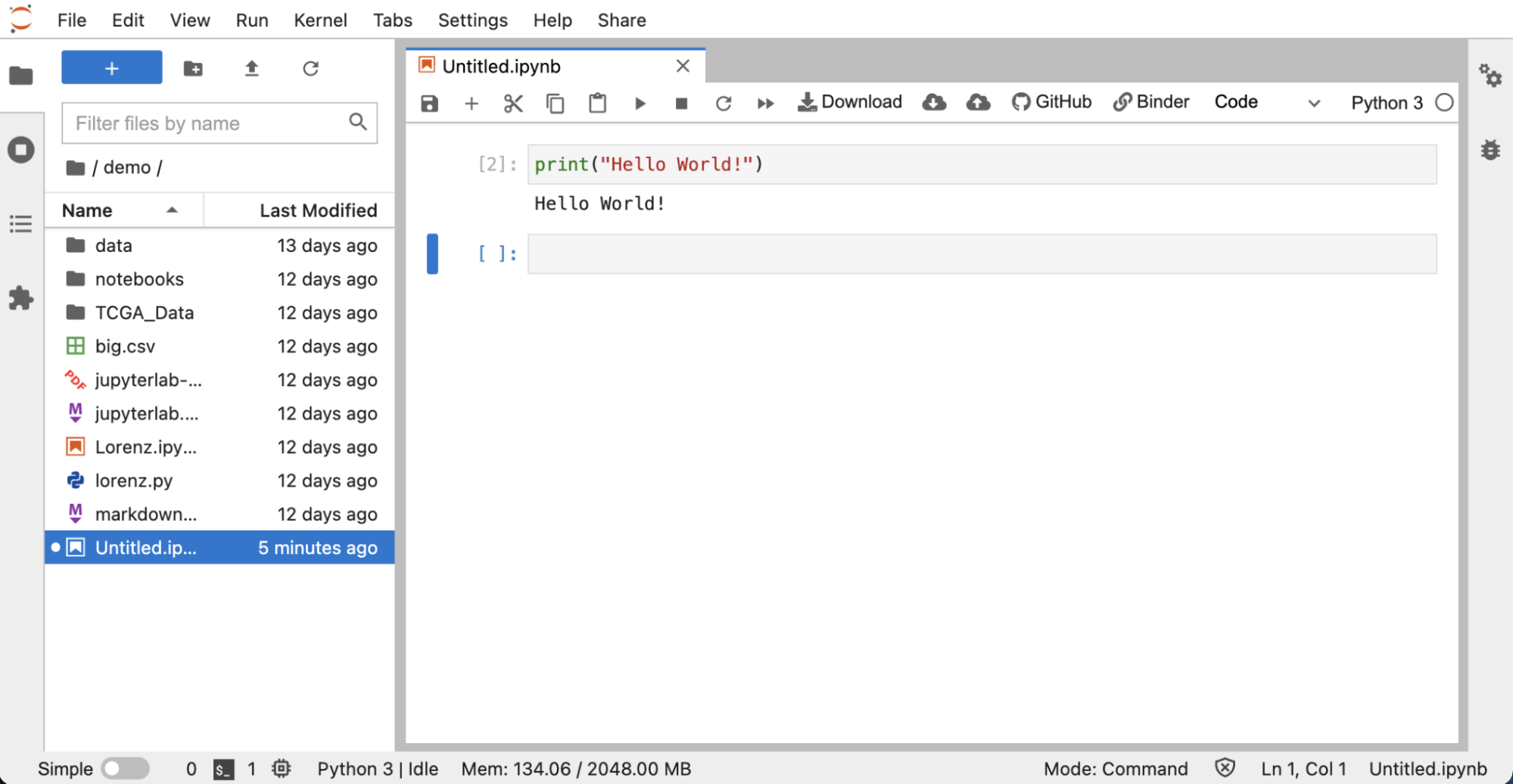
この記事では、Try JupyterのJupyterノートブックを用いて、実際に計算しながら解説を行う。まずはTry JupyterのURL( https://jupyter.org/try)にアクセスし、「JupyterLab」を選択し、[File]メニューから[New Notebook] – [Python3]をクリックして、Pythonのノートブック環境を開いてみよう。ノートブックのセルに

				print("Hello World!")

と入力し、[Run]をクリック（あるいは、セルを選択した状態でShift+Enter）し、以下のような「Hello World!」という文字が表示されていれば、Try Jupyterの導入は成功である。Pythonプログラミングに関する詳細は、参考文献1.に示すような入門講座を参照いただきたい。

太陽の周りを回る地球の軌道

速いスピードで走っている車が急には止まれないように、物体の運動は「慣性の法則」に支配されている。地上を走る車は、道路からの摩擦・車軸の摩擦・空気抵抗等で放っておいても徐々に減速するし、アクセルを踏めば加速する。もし、これらの摩擦力・空気抵抗力やアクセルによる加速がなければ、車は等速直線運動を続ける。初期時刻を $t_0$ 、初期位置を $\vec{r}_0$ 、初期速度 $\vec{v}_0$ としたとき、等速直線運動を続ける物体の時刻 $t$ における速度 $\vec{v}$ ・位置 $\vec{r}$ を数式で書くと以下のようになる。

\left\{ \begin{alignedat}{2} \vec{v}&=\vec{v}_{0}=\textrm{const}.\\ \vec{r} &= \vec{r}_0 + \vec{v}(t-t_0) \end{alignedat}\right.

シンプルな数式なので手計算の方が簡単だが、ここではあえてプログラミングで物体の運動を計算をしてみよう。単位を気にしないが、今後の計算と揃えて、距離をkm、時間をsとする。

# Pythonもモジュールを読み込み
import numpy as np # 数値計算ライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ

# 初期条件の設定
r0 = np.array([1.05782e8, 1.05782e8]) # 初期位置, km
t0 = 0 # 初期時刻, s
v0 = np.array([-21.06, 21.06]) # 速度ベクトル, km/s

# 時刻tにおける位置の計算
r = np.zeros((365,2)) # 1年分(=365日)計算
v = np.zeros((365,2)) # 1年分(=365日)計算
for i in range(365):
	t_sec = i*86400 # 1日を秒に換算 
	v[i,:] = v0
	r[i,:] = r0 + v[i,:]*(t_sec-t0)

# 描画
plt.plot(r[:, 0],r[:, 1], 'b')
plt.grid() # 格子をつける
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.xlabel('x, km')
plt.ylabel('y, km')
plt.show()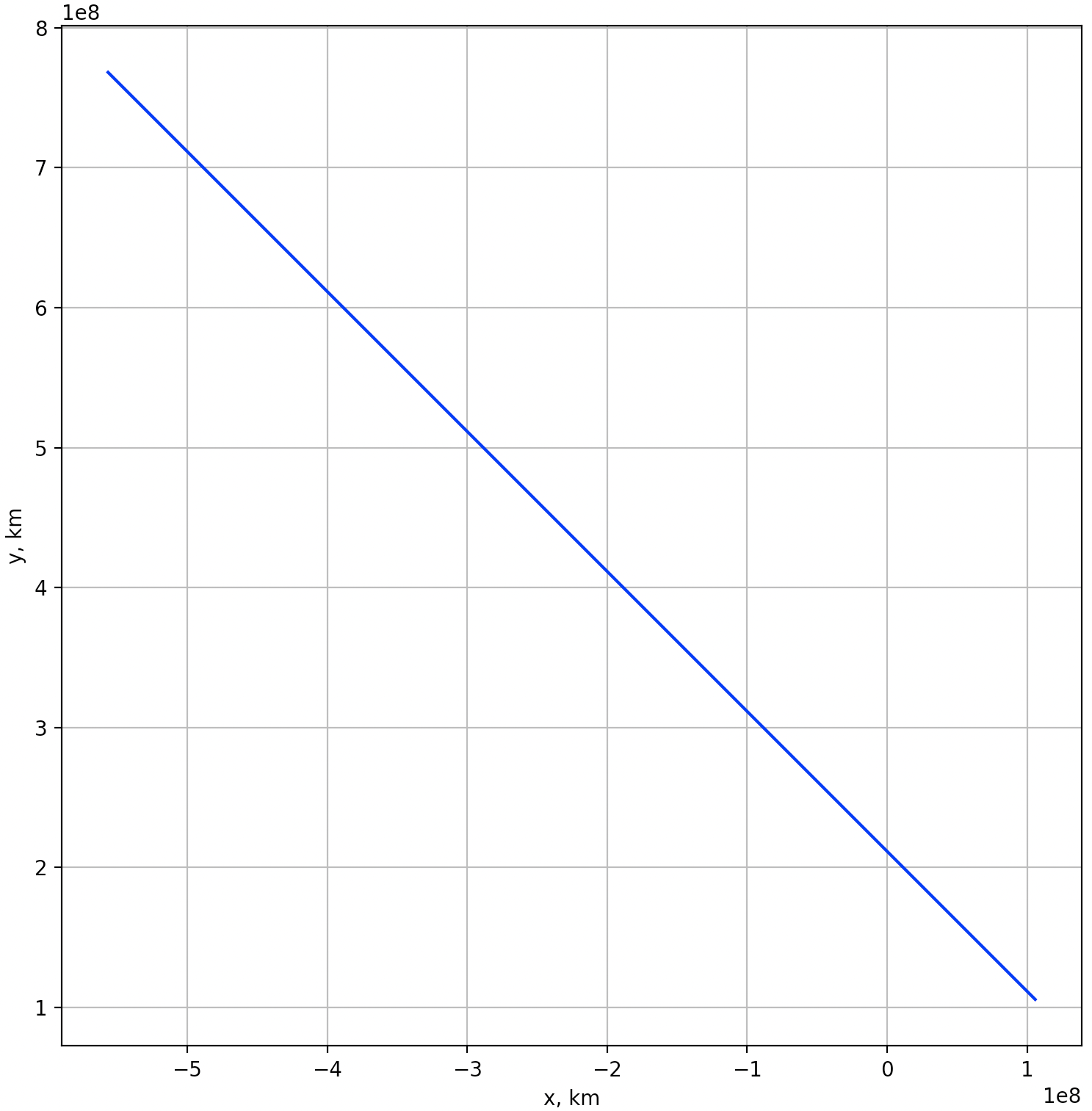

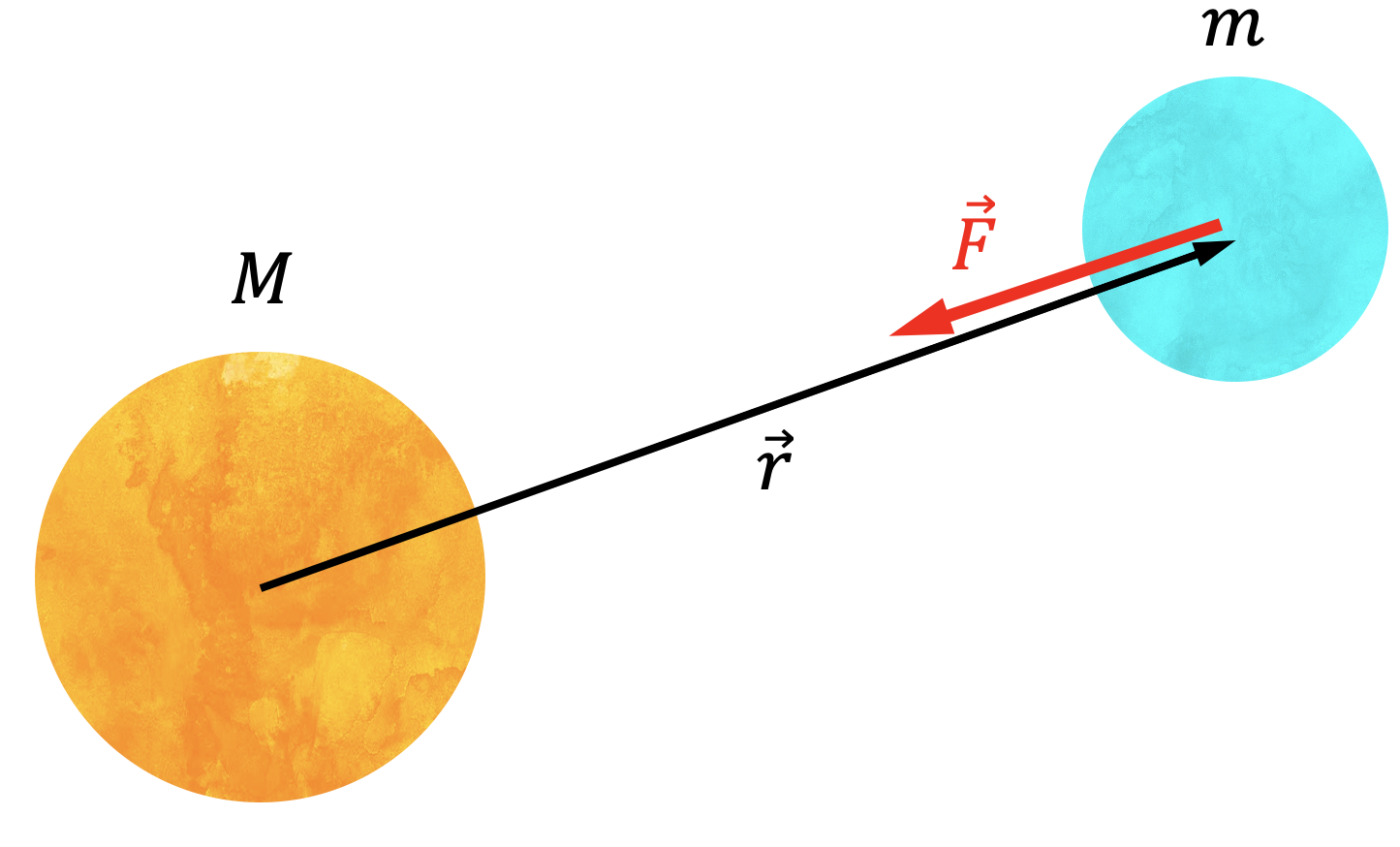
地球も秒速約30キロメートルという速度で運動している。宇宙空間は真空状態で空気抵抗もなく、何かから摩擦を受けることもない。そのまま何もなければ、等速直線運動を続けそうだが、実際には太陽を中心とした（円軌道に近い）楕円軌道を描いていることが観測されている。”何か”が地球の軌道を曲げているのである。イギリスの科学者アイザック・ニュートンは、「リンゴが木から落ちる現象（＝地球上の物体が落下する現象）」と「地球（や他の惑星）が太陽を中心とした楕円軌道を描く現象」が同じ法則によって支配されていることを発見した。これが「２つの物体の間には、物体の質量に比例し、物体間の距離の２乗に反比例する引力が作用する」という万有引力の法則である。数式で表すと、距離 $r$ だけ離れた質量 $M$ と質量 $m$ の物体の間に

F=G\frac{Mm}{r^2}

という力 $F$ が作用していることになる。ここで $G$ は万有引力定数という比例係数であり、観測の結果 $G=6.67430(15)×10^{−11} \textrm{m}^3 \textrm{kg}^{−1} \textrm{s}^{−2}$ であることが分かっている。ベクトルを用いて表現すると、引力は

\vec{F}=-G\frac{Mm}{r^3}\vec{r}

となる。万有引力 $\vec{F}$ は距離 $\vec{r}$ と反対の向きに加わるので、 $-\frac{\vec{r}}{r}$ が掛け算されている（ベクトルの大きさを変えないようにするために、 $\vec{r}$ を $r$ で割っている）。

ニュートンは更に運動の第２法則と呼ばれる「物体の運動状態の時間変化と物体に作用する力の関係を示す法則」を唱えた。この法則によると、質量 $m$ の物体が力 $\vec{F}$ を受けると、その力の方向に加速度 $\vec{a}$ （＝単位時間辺りの速度変化量）が生じ、それらの間には以下の関係がある。

m\vec{a}=\vec{F}

これらの数式について「なぜこのような数式になるのか？」気になる読者がいるかもしれないが、残念ながら観測に基づいて導き出された”法則”なので、別の原理から導出できるものではない。また、あくまで観測結果から「正しそうだ」というだけであって、絶対的に正しいわけではない。実際に水星の軌道計算をすると僅かに誤差が生じることが分かっており、アインシュタインの相対性理論によりニュートンの法則の不完全性が示された。なので、特に科学者を志している人は、常に疑って欲しい。一方で、技術者を志している人は、実用性を見るべきである。軌道設計をする上では、特別に高い精度を求めない限りは、ニュートンの法則が実用的に十分である。やはりニュートンは偉大である。

さて、運動の第２法則と万有引力の法則から、質量 $M$ の物体が質量 $m$ の物体に与える加速度は以下の式で計算できる。

\vec{a}=-\frac{GM}{r^3}\vec{r}

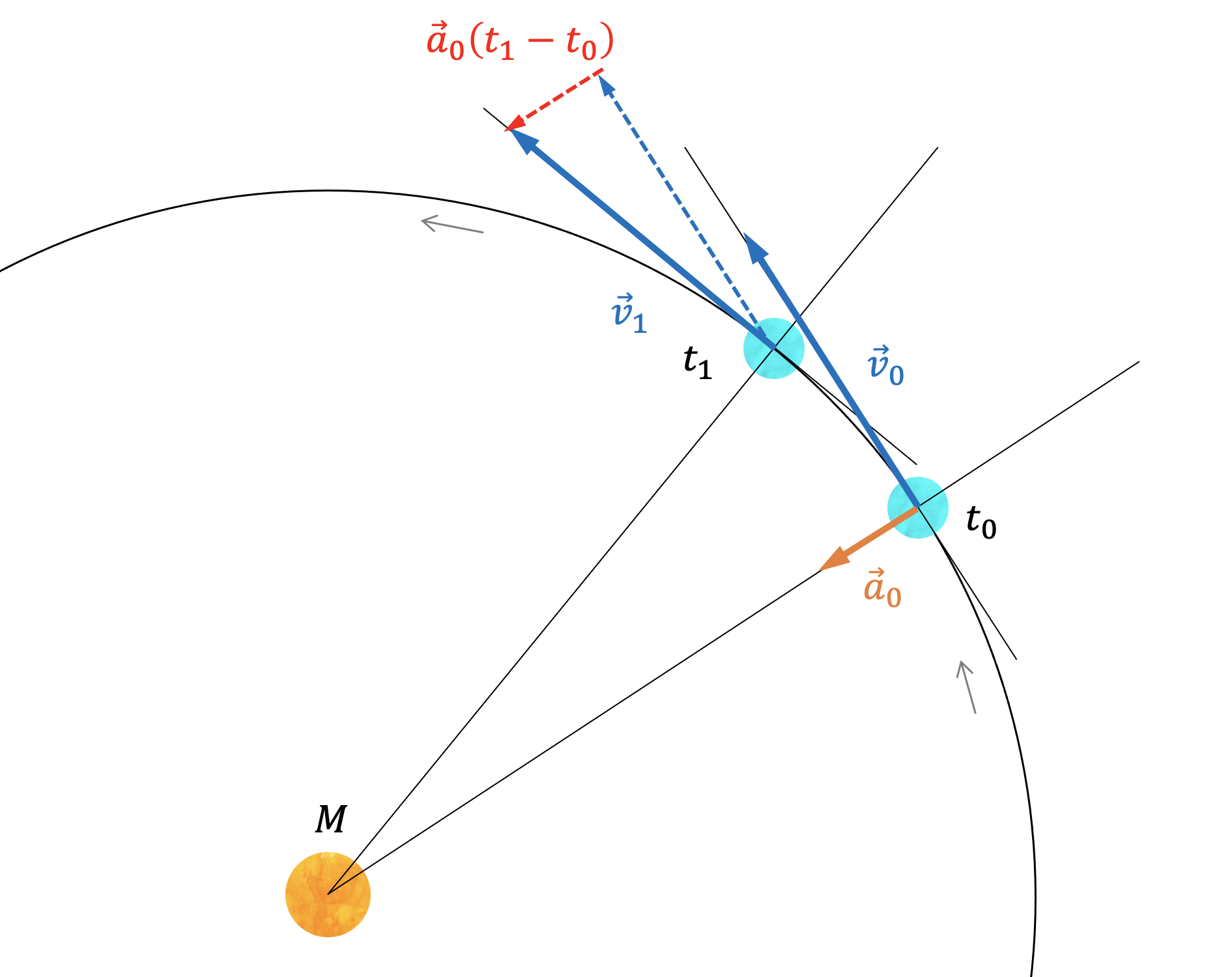
時刻 $t_0$ において速度 $\vec{v}_0$ で運動をしている物体に、万有引力による加速度 $\vec{a}_0$ が作用している状態を考える。加速度とは単位時間あたりの速度変化量なので、時刻 $t_1$ における速度 $\vec{v}_1$ は、以下の式で概算できる。

\begin{align*} \vec{v}_1&=\vec{v}_0 + \vec{a}_0(t_1-t_0)\\ &=\vec{v}_0 -\frac{GM}{r_0^3}\vec{r}_0(t_1-t_0) \end{align*}

等速直線運動の計算と同様に、位置の計算と合わせて表記すると以下の式となる。

\left\{ \begin{alignedat}{2} \vec{v}_1&=\vec{v}_0 -\frac{GM}{r_0^3}\vec{r}_0(t_1-t_0)\\ \vec{r}_1 &= \vec{r}_0 + \vec{v}_0(t_1-t_0) \end{alignedat}\right.

ここでは時刻 $t_0$ から時刻 $t_1$ までの運動を考えたが、数列のように繰り返し計算をすることで任意の時刻 $t_i$ における位置 $\vec{r}_i$ と速度 $\vec{v}_i$ を計算することができる。別の言葉で言うと、数列 $\vec{r}_i, \vec{v}_i$ を再帰的に計算するための漸化式となっているのである。早速プログラミングで計算してみよう。

# Pythonもモジュールを読み込み
import numpy as np # 数値計算ライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ

# 条件の設定
GM = 1.327e11 # 万有引力定数×中心天体の質量, km^3/s^(-2)
t0 = 0 # 初期時刻, s
r0 = np.array([1.05782e8, 1.05782e8]) # 初期位置, km
v0 = np.array([-21.06, 21.06]) # 速度ベクトル, km/s

# 時刻tにおける位置の計算
t = np.zeros(365) # 1年分(=365日)計算
r = np.zeros((365,2)) # 1年分(=365日)計算
v = np.zeros((365,2)) # 1年分(=365日)計算

# 初期条件の代入
t[0] = t0
r[0,:] = r0
v[0,:] = v0

# 繰り返し計算
for i in range(364):
    r0_norm = np.sqrt(r[i,0]**2 + r[i,1]**2)
    t[i+1] = t[i] + 86400 # 1日分加算
    v[i+1,:] = v[i,:] - GM*r[i,:]*(t[i+1]-t[i])/(r0_norm**3)
    r[i+1,:] = r[i,:] + v[i,:]*(t[i+1]-t[i])

# 描画
plt.plot(r[:, 0],r[:, 1], 'b')
plt.grid() # 格子をつける
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.xlabel('x, km')
plt.ylabel('y, km')
plt.show()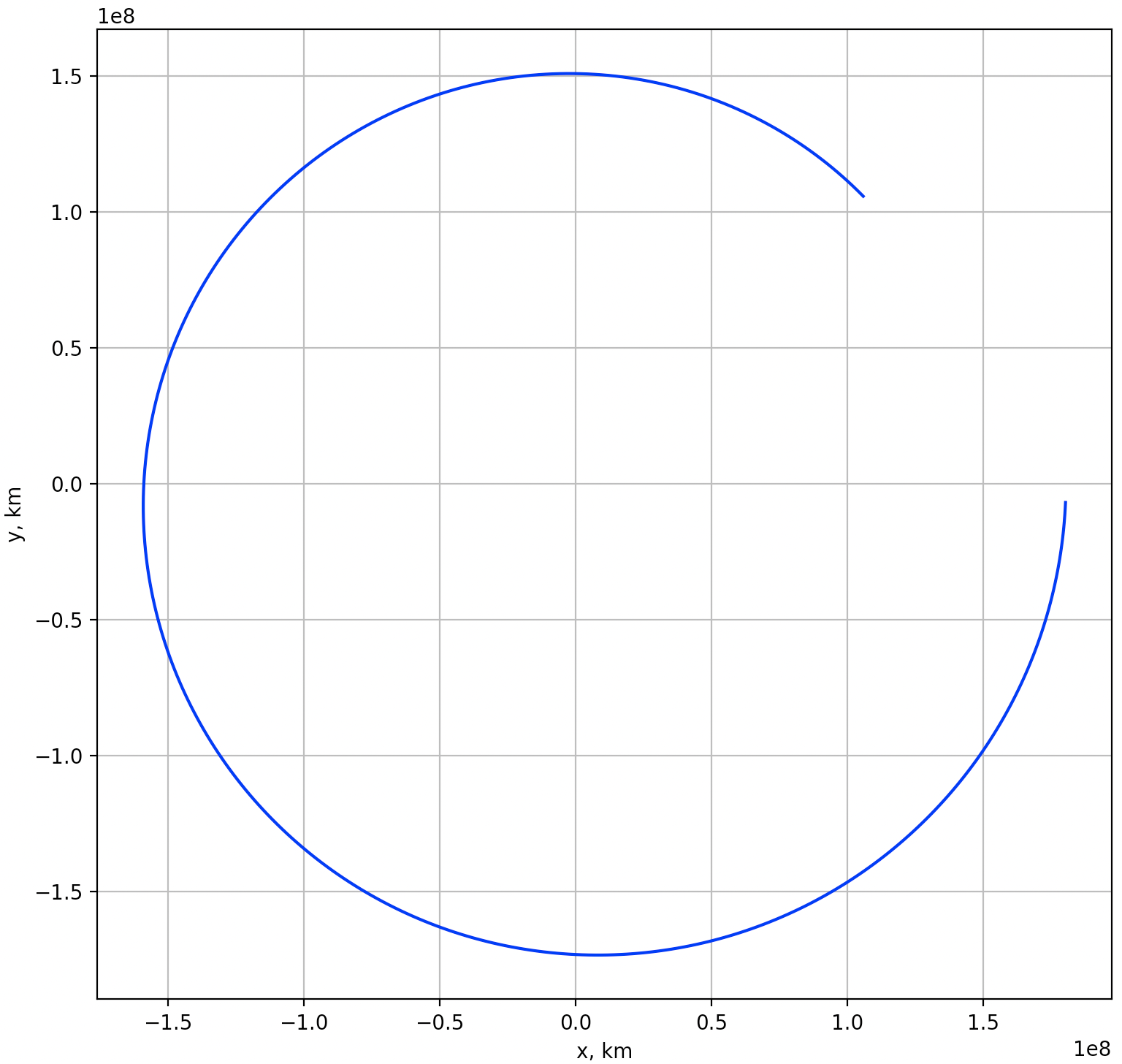

さっきは等速直線運動していた物体の運動が太陽の重力によって曲がっていることが確認できただろうか？とはいえ、本当は太陽の周りを回る地球の軌道を描きたかったはずだが、綺麗な（円に近い）楕円軌道にはなっていないことが分かる。なぜこのような誤差が生じたのか考察をしたいと思う。ここまでの式展開の過程で違和感はなかっただろうか？万有引力による力は連続的に加わるはずなのに、 $t_0$ から $t_1$ の間で一定の加速度（ $=\vec{a}_0$ ）が加わり続けるような定式化になっている。同様に、速度は $t_0$ から $t_1$ の間で時々刻々と変わるはずなのに、一定の速度（ $=\vec{v}_0$ ）を前提に位置が計算されている。まさに、これが誤差の原因となっている。この誤差を小さくするためには、時間の刻み幅（ $t_0$ と $t_1$ の差）を小さく（細かく）し、位置・速度がスムーズに変化するようにすれば良い。

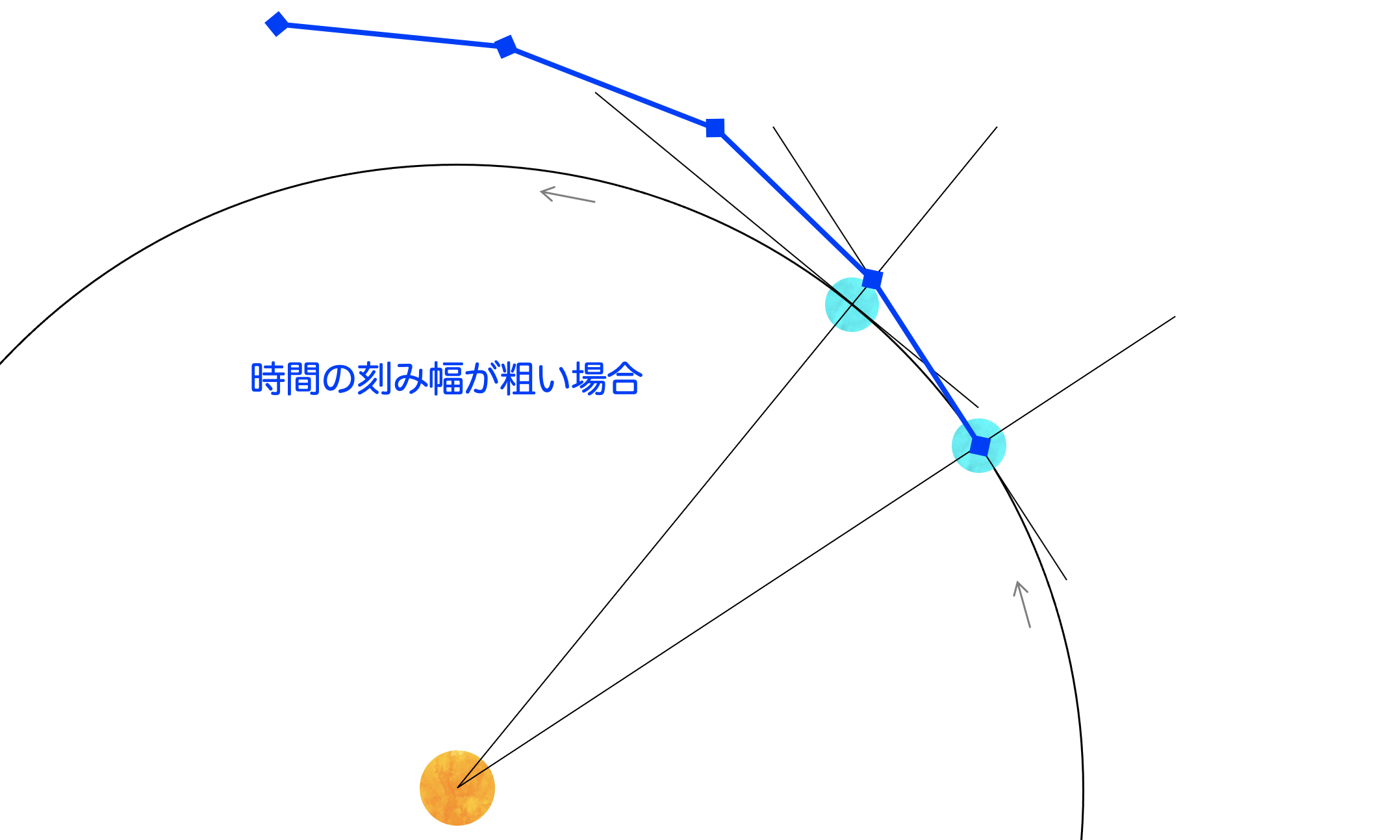
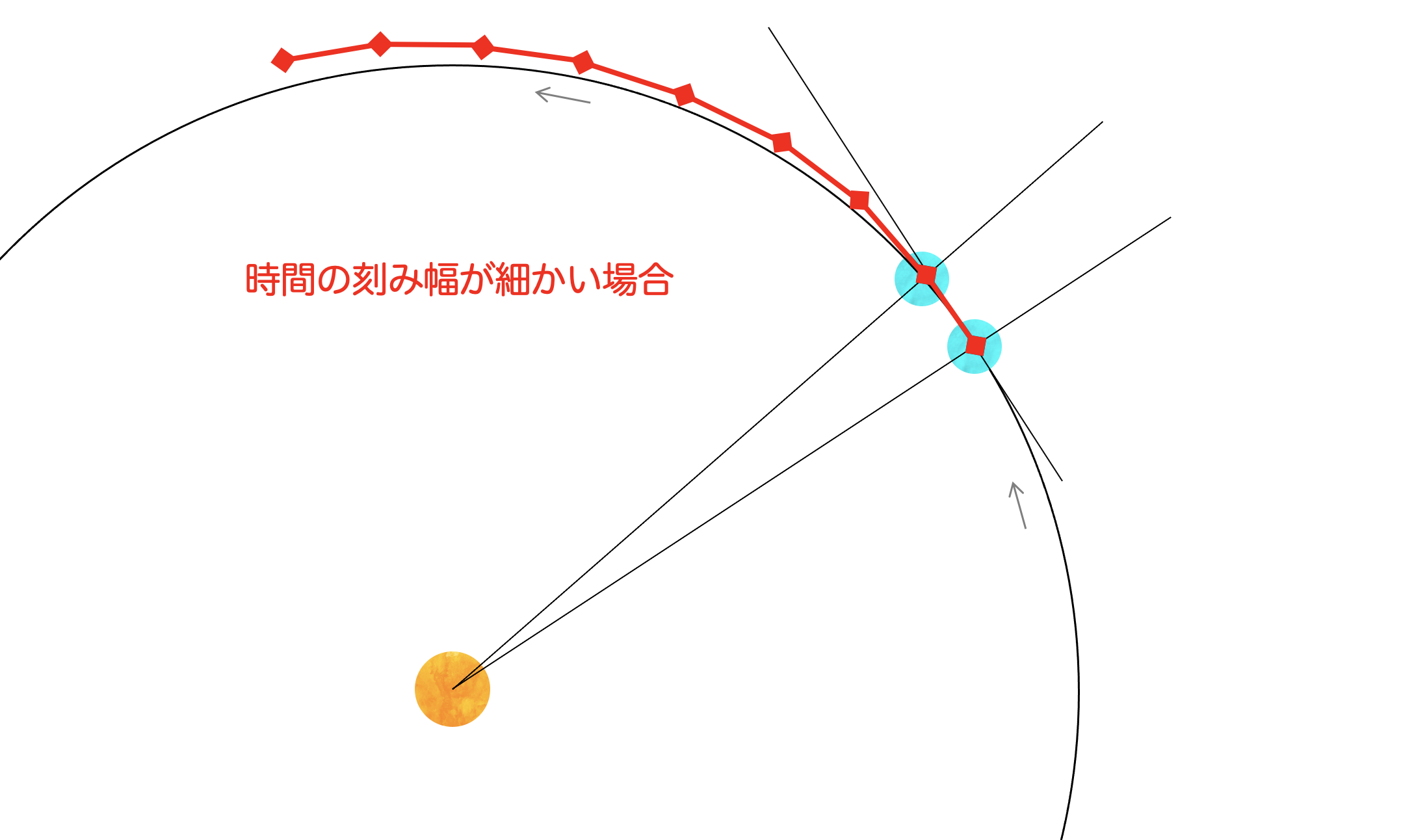
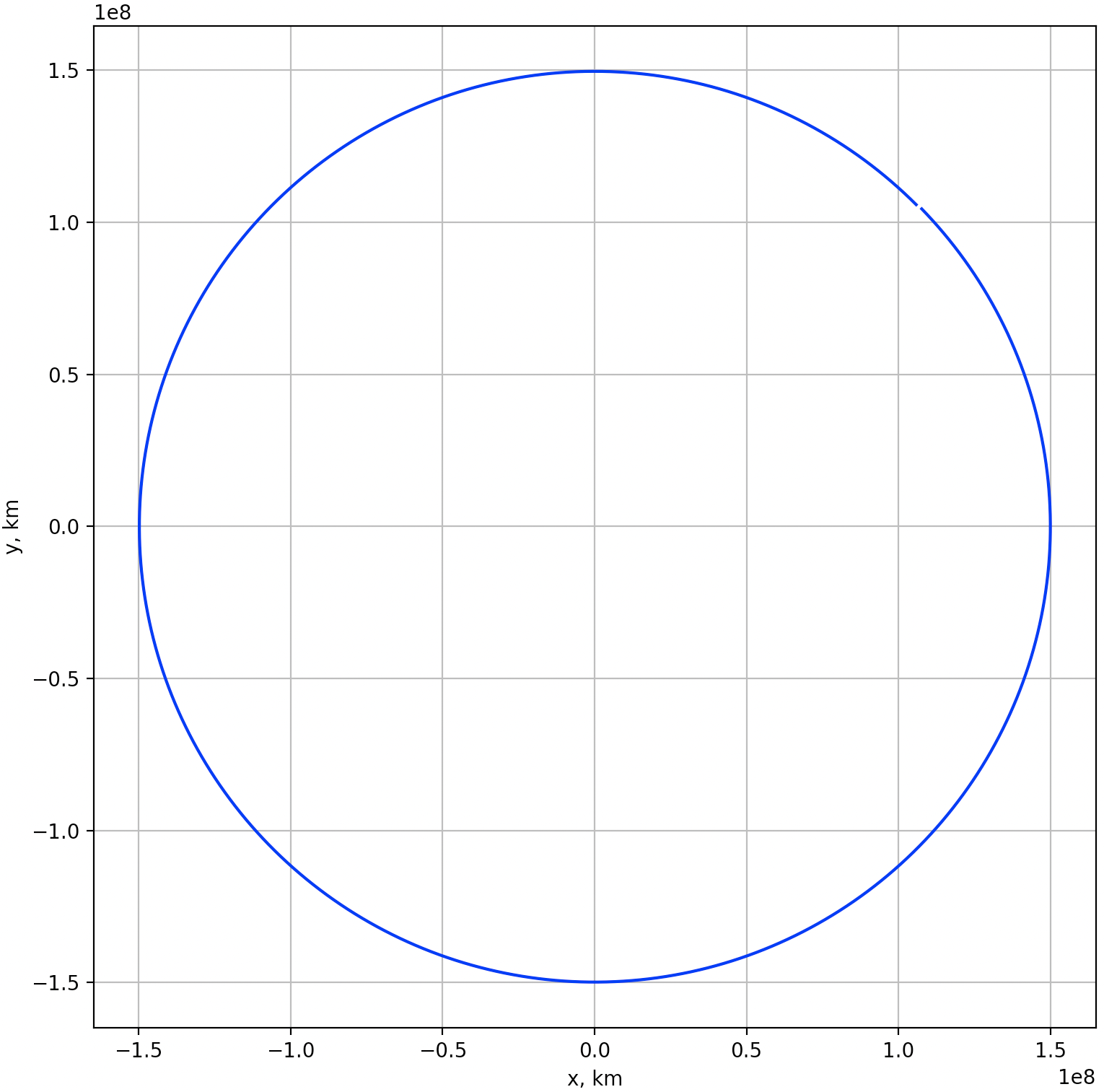
例えば、1日刻みで設定していた幅を、864秒刻み（＝100分の1）にしてみよう。すると、以下のような綺麗な楕円軌道が描けることが分かる。これが軌道計算の第一歩である！このようにある時刻の位置・速度から別の時刻の位置・速度を計算することを軌道伝播と呼ぶ。我々専門家は日々、軌道伝播をしている。

漸化式から微分方程式へ

さて時間の刻み幅が細かくすると誤差が小さくなるわけだが、時間の刻み幅を極限まで小さくすると何が起こるだろうか？プログラム上は計算時間が無限に掛かってしまうことになる（少し試してみて欲しい）が、数式上の考察は可能である。

\left\{ \begin{alignedat}{2} \vec{v}_1&=\vec{v}_0 -\frac{GM}{r_0^3}\vec{r}_0(t_1-t_0)\\ \vec{r}_1 &= \vec{r}_0 + \vec{v}_0(t_1-t_0) \end{alignedat}\right.

の $t_1$ を極限まで $t_0$ に近づけてみる。すると、 $(t_1-t_0)$ は $0$ になるため、 $\vec{v}_1=\vec{v}_0$ 、 $\vec{r}_1=\vec{r}_0$ というあまり価値のない式が得られる。そこで、時間に対する変化率に着目して、式展開をしてみる。

\left\{ \begin{alignedat}{2} \frac{\vec{v}_1- \vec{v}_0}{t_1-t_0}&= -\frac{GM}{r_0^3}\vec{r}_0\\ \frac{\vec{r}_1- \vec{r}_0}{t_1-t_0} &= \vec{v}_0 \end{alignedat}\right.

この式において、 $t_1$ を極限まで $t_0$ に近づけてみる。左辺は $\frac{0}{0}$ となり、値が定義できない不定形にみえるが、右辺は具体的な値が定義できる数式となっている。そこで、よく分からない左辺を以下のように書き換えることにする（それと合わせて、 $r_0, v_0$ の添え字の0を省略する）。

\left\{ \begin{alignedat}{2} \frac{d\vec{v}}{dt}&= -\frac{GM}{r^3}\vec{r}\\ \frac{d\vec{r}}{dt} &= \vec{v} \end{alignedat}\right.

この $\frac{d\square}{dt}$ を $\square$ の時間微分とよぶ。微分と聞くと拒否反応を示す人は”時間に対する変化率”と読み変えても大丈夫である。位置の時間微分（＝時間に対する変化率）は速度、速度の時間微分（＝時間に対する変化率）は加速度、という関係が得られることが分かる。このように微分を含む方程式を、微分方程式と呼ぶ。微分方程式の解き方に関して、これまで様々な学者が研究してきており、数値的に計算するPythonライブラリが提供されている。ライブラリとは、図書館を意味する英単語だが、プログラミング分野においては、先人たちが作成してきたプログラムを他のプログラムが引用できる状態にしたものを指す。そのライブラリの1つであるscipy.integrateのodeintを使って、軌道伝播してみよう。以下の数値計算では、位置 $\vec{r}$ (2次元)と速度 $\vec{v}$ (2次元)を合わせて、 $\vec{x}$ という1つの4次元ベクトルで表現する。

# Pythonもモジュールを読み込み
import numpy as np # 数値計算ライブラリ
from scipy.integrate import odeint # 常微分方程式を解くライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ

# 軌道の運動方程式
def func(x, t):
	GM = 1.327e11 # 万有引力定数×中心天体の質量, km^3/s^(-2)
	r_norm = np.sqrt(x[0]**2 + x[1]**2)	
	dxdt = [x[2], 
				  x[3], 
					-GM*x[0]/(r_norm**3),
					-GM*x[1]/(r_norm**3)]
	return dxdt

# 初期条件の設定
x0 = np.array([1.05782e8, 1.05782e8,-21.06, 21.06]) # 位置, 速度, km, km/s
t = np.linspace(0,365*24*60*60,100) # 1年分を100ステップで刻む

# 微分方程式の数値計算
sol = odeint(func, x0, t)

# 描画
plt.plot(sol[:, 0],sol[:, 1], 'b')
plt.grid() # 格子をつける
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.xlabel('x, km')
plt.ylabel('y, km')
plt.show()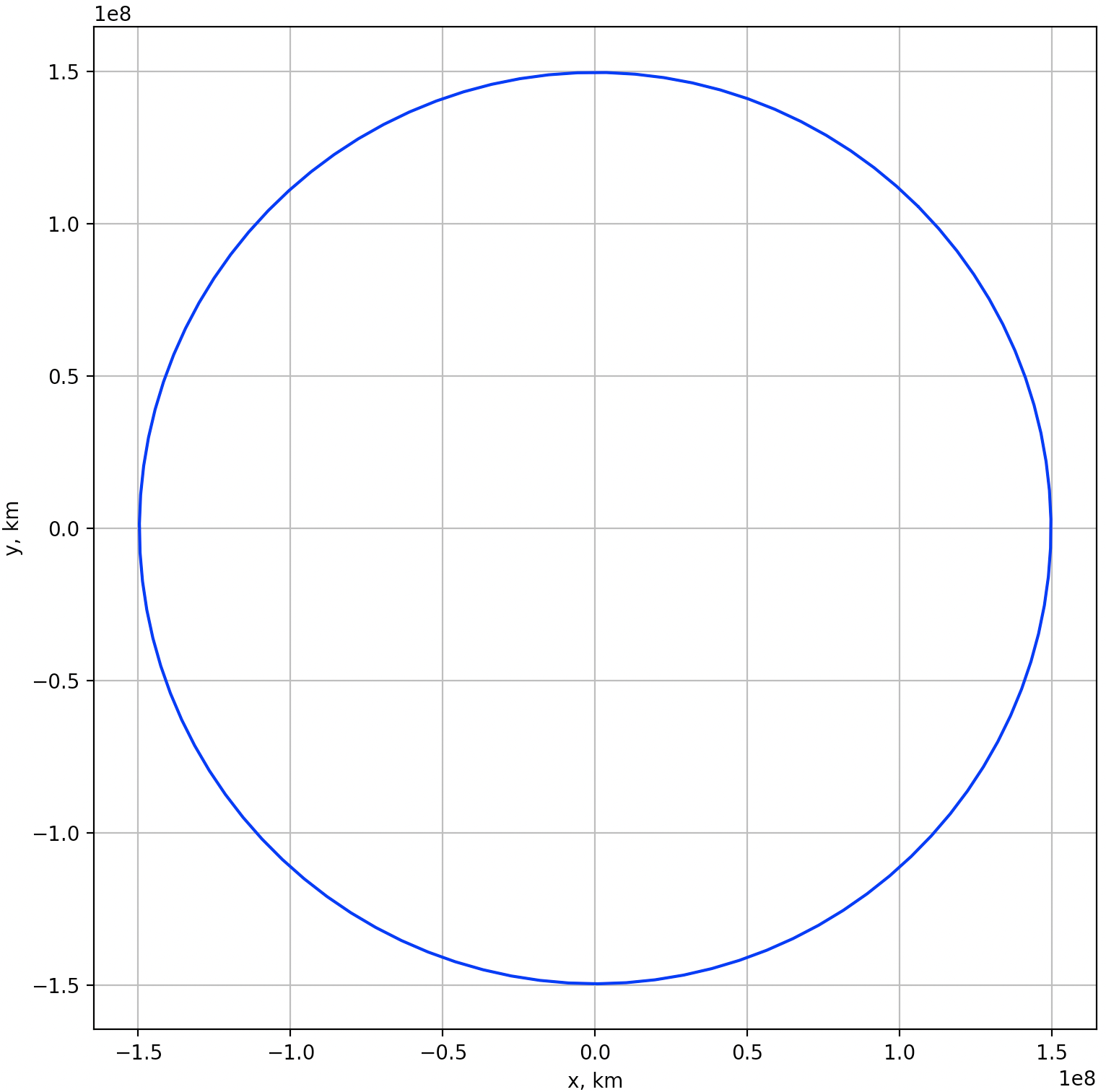

より発展的な内容に興味がある読者は、

初期条件を変えると何が起こるか？

ケプラーの法則やエネルギー保存則が成り立っているか？

3次元に拡張するとどうなるか？

座標系を変えて軌道を描いてみるとどうなるか？

等を試してみていただきたい。また、Pythonを用いた人工衛星・宇宙機の軌道力学に関して、更に興味がある読者は宙畑の記事2〜4を参考にしていただきたい。

まとめ

今回は、高校数学・物理の知識とPythonプログラミングに関する入門的な知識を用いて、軌道伝播プログラムを実装した。ご覧のとおり、軌道設計は、数学・物理・プログラミングが複合的に合わさった応用問題となっている。軌道設計というと非常にニッチな分野に思われるかもしれないが、宇宙ミッションを考える上で最初に求められることが軌道設計であるため、宇宙を志す者の教養として知っておいて損はない。次回は、いよいよスイングバイの軌道設計に取り組もう。

参考文献

“ゼロからのPython入門講座"、https://www.python.jp/train/index.html、アクセス日：2022年7月30日

尾崎直哉、”人工衛星の軌道を徹底解説！軌道の種類と用途別軌道選定のポイント”、宙畑、2021年10月6日、（https://sorabatake.jp/23000/、アクセス日：2022年7月30日）

尾崎直哉、”Pythonを使って人工衛星の軌道を表現する～軌道６要素、TLE～”、宙畑、2021年10月28日、（https://sorabatake.jp/23655/、アクセス日：2022年7月30日）

尾崎直哉、”人工衛星の軌道の種類～目的地としての軌道と移動ルートとしての軌道～”、宙畑、2021年11月24日、（https://sorabatake.jp/24030/、アクセス日：2022年7月30日）

著者情報

尾崎直哉（Naoya OZAKI）
JAXA宇宙科学研究所
テニュアトラック特任助教・宇宙ミッションデザイナー・博士（工学、東京大学、2018年）。世界初の超小型深宇宙探査機PROCYON（プロキオン）の開発を中心に、多くの深宇宙探査ミッションに携わる。ESA・NASA・JAXAの３機関にて修行を積んだ軌道設計のスペシャリスト。

▶ JAXAacademy
▶ 提出詳細ページ