
著者:JAXA宇宙科学研究所 尾崎 直哉
高校数学・物理で学ぶスイングバイ軌道の作り方②
〜スイングバイの軌道計算をしてみよう〜
この記事では、高校数学・物理の知識とPythonプログラミングに関する入門的な知識から、”スイングバイ”を活用した軌道設計を行うまでのプロセスを丁寧に説明し、読者に実際に計算してもらうものである。軌道設計とは、人工衛星や探査機が飛行するルートを計画することである。旅行の計画を立てる際に、移動ルートを真っ先に考えなければいけないように、宇宙ミッションを考える際に、真っ先に考えなければいけないことが軌道設計である。この記事では、高校数学•物理の知識から出発し、この記事を読み終えた頃には、「はやぶさ」のような探査機の軌道設計ができる一歩手前まで到達してもらいたいと考えている。今回はN体問題の軌道伝播プログラムを用いて、スイングバイを用いた軌道設計をしてみよう。
N体問題の軌道設計へ
前回は、太陽の万有引力のみを考慮した地球の軌道について考えてきた。このように「太陽と地球」や「太陽と探査機」といった互いに相互作用を及ぼす2つの物体の運動を扱う問題を二体問題と呼ぶ。同様に「太陽と地球と探査機」といった互いに相互作用を及ぼす3つの物体の運動を扱う問題を三体問題、N個の物体の運動を扱う問題をN体問題と呼ぶ。ここまでで作成した二体問題の軌道伝播プログラムを発展させて、N体問題の軌道伝播プログラムを作成してみよう。N体問題の軌道計算をする方程式(運動方程式)は、第三天体・第四天体の万有引力による加速度を加えるだけで計算できる。すなわち、以下のような数式である。
ただし、この式は、中心天体(=太陽)は慣性座標系上に固定されていると仮定している。実際には、木星等の第天体の万有引力の影響を受けて、太陽の位置も変動する。
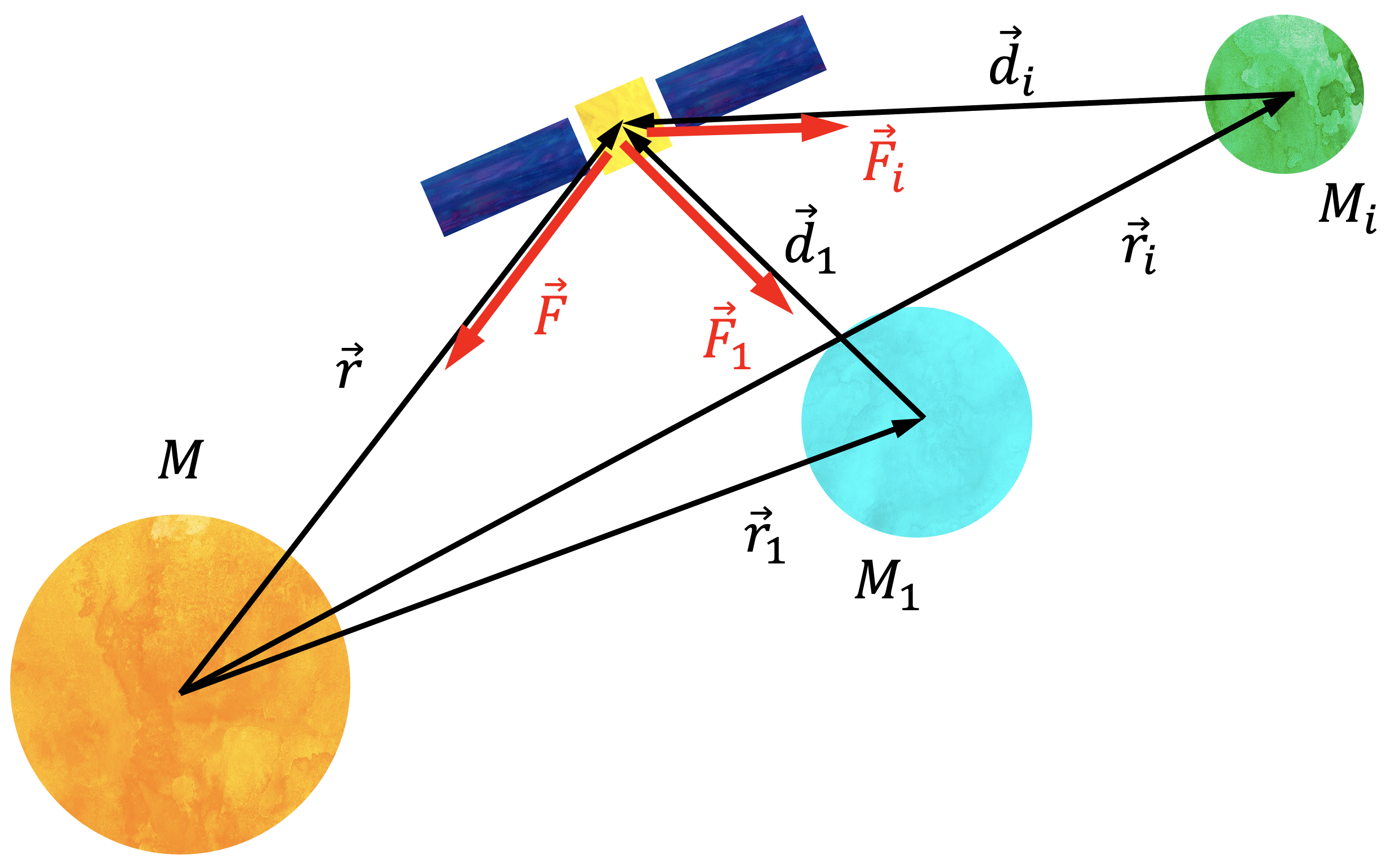
第番目の天体から探査機までの距離 は、中心天体に対する第 番目の天体の位置を用いて、
で計算される。では、第番目の天体の位置は、どのように計算できるだろう?我々専門家は、通常、エフェメリス(天体暦)と呼ばれる天体の(精密な)軌道を書き出した情報を用いて計算する。このエフェメリスを用いたアプローチは少し複雑なので、ここでは簡易化して計算することを考える。そこで、全ての惑星が太陽を中心とした同一平面内の円軌道で運動すると仮定する。すると、ある時刻 における惑星の位置
は、円(二次曲線の1つ)のパラメータ表示(媒介変数表示)を用いて以下のように計算できる。
ただし、は軌道半径、 は軌道周期、 は初期時刻( )における惑星の位相を表す。は時刻 における惑星の位相を表している。では、早速、Pythonのプログラミングで動作確認をしてみよう。問題を簡易化するために、太陽と地球の重力のみを考えるが、発展的な内容に興味がある読者は、さらに惑星を増やして考えてみてもらいたい。
# Pythonもモジュールを読み込み
import numpy as np # 数値計算ライブラリ
from scipy.integrate import odeint # 常微分方程式を解くライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ
# N体問題の運動方程式
def func_nbody(x, t):
# 条件設定
GM = 1.327e11 # 万有引力定数×太陽の質量, km^3/s^(-2)
GM1 = 3.986e5 # 万有引力定数×地球の質量, km^3/s^(-2)
theta1 = 44*(np.pi/180) # テキトーに44degと設定, deg -> rad
period1 = 365*24*60*60 # 地球の軌道周期, sec
a1 = 149597870.7 # 地球の軌道長半径, km
# 地球の位置
r1 = np.array([ a1*np.cos(2*np.pi*t/period1 + theta1),
a1*np.sin(2*np.pi*t/period1 + theta1) ])
# 運動方程式の計算
d1 = x[0:2] - r1
r_norm = np.sqrt(x[0]**2 + x[1]**2)
d1_norm = np.sqrt(d1[0]**2 + d1[1]**2)
if d1_norm < 6371: # 地球距離が地球半径以下になると衝突してしまうため、エラーを返す
print("ERROR: 地球スイングバイ時の高度がマイナスです!")
dxdt = [x[2],
x[3],
-GM*x[0]/(r_norm**3) - GM1*d1[0]/(d1_norm**3),
-GM*x[1]/(r_norm**3) - GM1*d1[1]/(d1_norm**3)]
return dxdt
# 条件の設定
x0 = np.array([1.05782e8, 1.05782e8,-21.06, 21.06]) # 位置, 速度, km, km/s
t_span = np.linspace(0,365*24*60*60,100) # 1年分を100ステップで刻む
# 微分方程式の数値計算
sol = odeint(func_nbody, x0, t_span)
# 描画
plt.plot(sol[:, 0],sol[:, 1], 'b')
plt.grid() # 格子をつける
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.xlabel('x, km')
plt.ylabel('y, km')
plt.show()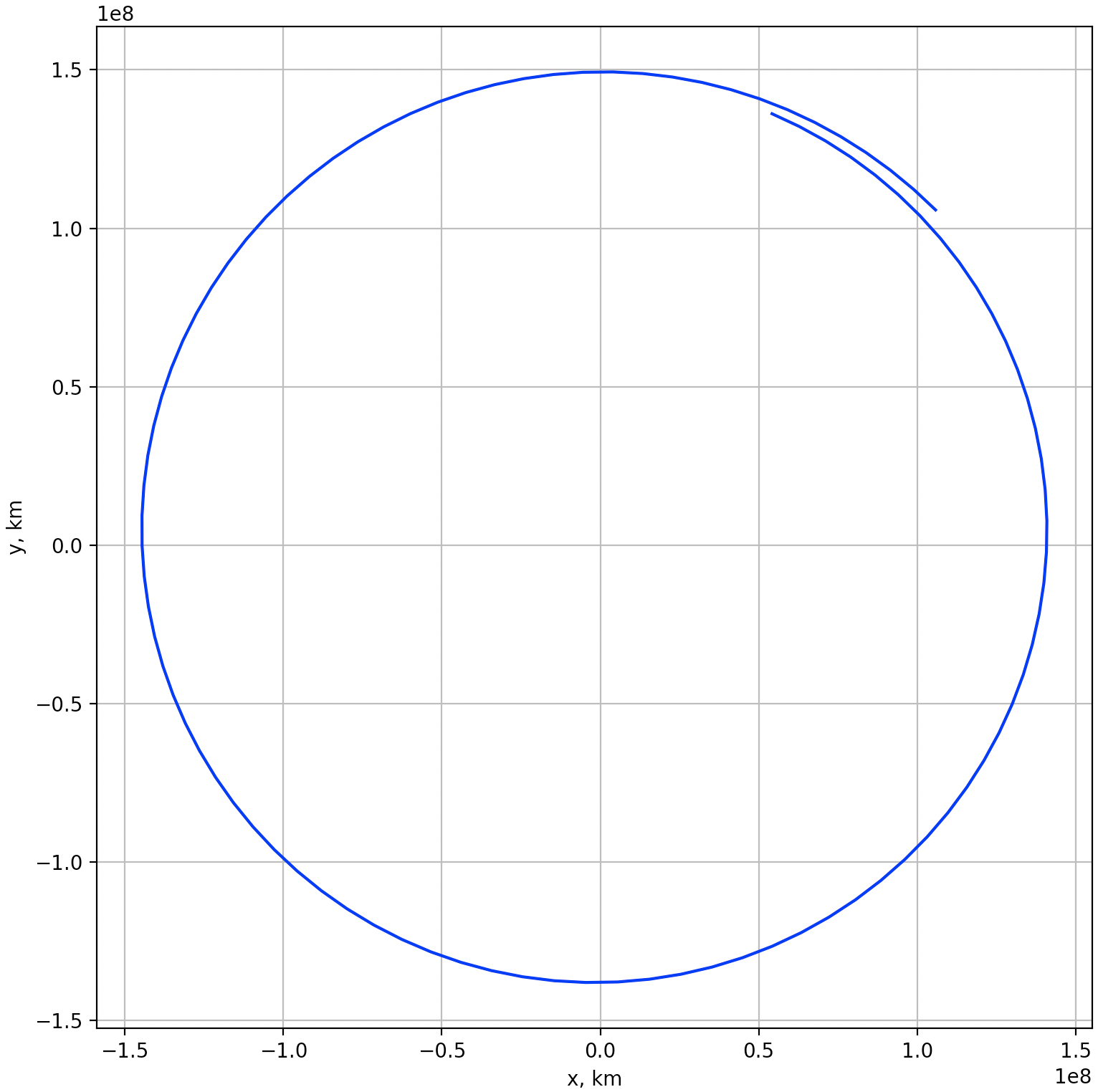
先ほどの二体問題の場合と同じ初期条件のはずなのに、閉じた円にはならず、軌道が少しズレていることが確認できるだろうか?まさに、地球の重力の影響で、探査機の軌道が曲げられてしまったのである!ここまで来ると、スイングバイの軌道設計まで、あと一歩である。
「はやぶさ」のような地球スイングバイ軌道の設計
スイングバイを活用した軌道の一例として、「はやぶさ」が用いたような地球スイングバイ軌道設計について考えよう。「はやぶさ」では、地球から打ち上げられて、約1年後に地球に再接近して、地球スイングバイをする軌道が採用されている。この約1年間の間にイオンエンジンを用いた軌道制御を加えた後に地球スイングバイを行うことで、直接的に地球から打ち上げるよりも効率的に地球離脱を行うことができる。1年間に蓄積した軌道制御量を、数倍にして、地球スイングバイのときに一気に解放できるという軌道設計のワザである。このようなワザをEDVEGA(Electric Delta-V Earth Gravity Assist)とかV∞レベレージング(V-Infinity Leveraging)と呼ばれることがある。
地球を出発して1年後に地球に再接近する軌道
探査機が地球を出発して、1年後に地球に再接近する軌道を設計してみよう。ここからは実際にプログラムを書くまでの間、(地球や他の惑星の重力を無視した)太陽に対する二体問題を仮定する。
地球の(公転)軌道周期は1年なので、「出発時の地球位置」と「再接近時の地球位置」は、同じになっているはずである。つまり、探査機側も同じ位置を出発し、1年後に同じ位置に戻ってくるような軌道でなければいけない。これは言い換えると、探査機の軌道周期も1年ということを意味する。正確には、探査機の軌道周期が1/2年や 年であっても、探査機が太陽の周りを2周や 周してから、地球に戻ってこれば、このような軌道は成立する。さらに一般化すると、「地球の軌道周期」と「探査機の軌道周期」が、整数比になっていれば、このような軌道は成立する。このような軌道を我々専門家は共鳴軌道(Resonant Orbit)と呼んでいる。ここでは、最もシンプルな例として、地球と探査機の軌道周期が共に1年の例を考える。
ここで、ケプラーの第3法則を思い出してみよう。
ケプラーの第3法則:惑星の公転軌道周期の2乗は、軌道長半径 (=楕円軌道の長軸方向の半径)の3乗に比例する。
数式で表すと
ただし、は太陽の周りを回る惑星・探査機で全て同じ値である。このケプラーの第3法則は、ニュートンの運動方程式と万有引力の法則から導き出せる(歴史的には、ケプラーの法則を元に、ニュートンが諸々の法則を思いついたわけだが)。
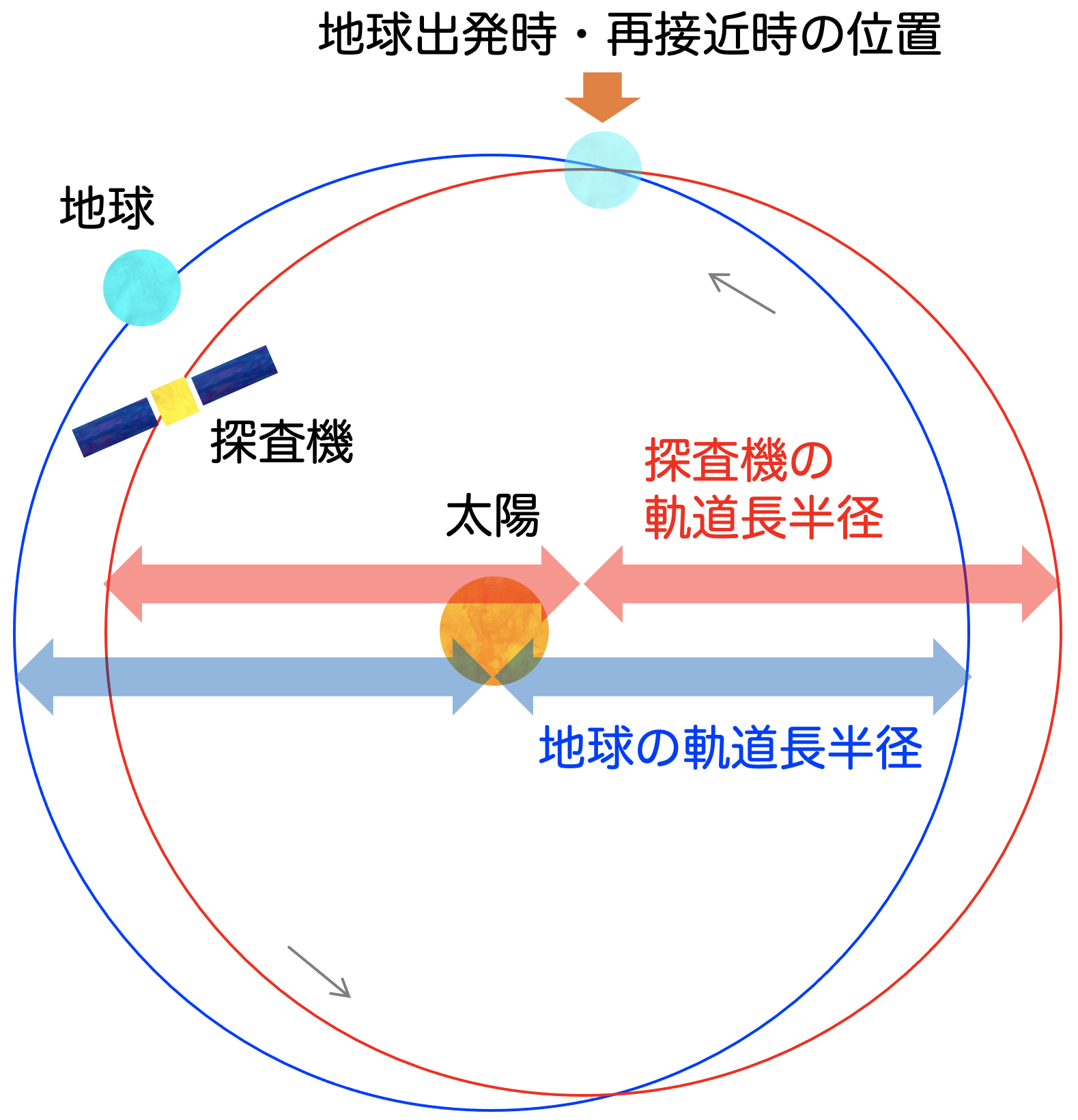
地球の軌道周期と探査機の軌道周期が一致している(=共に1年)ということは、地球の軌道長半径と探査機の軌道長半径が一致していることを意味する。すなわち、以下の図のような状態である。
共鳴軌道の軌道伝播をしてみよう
ここまでで地球に対する共鳴軌道を飛行する探査機の軌道が幾何学的にどのようなものか理解できただろうか。具体的に探査機の軌道を伝播し、軌道設計を行うには、探査機の初期位置と初期速度が必要である。探査機の地球出発を初期条件とすると、探査機の初期位置は地球の初期位置とほぼ同じである。あとは初期速度が計算されれば、探査機の軌道伝播が可能である。初期速度を計算するためには、軌道のエネルギー保存則を用いる。
ただし、は一定値であることを表し、左辺第1項は運動エネルギー、左辺第2項は位置エネルギー(ポテンシャルエネルギー)である。この軌道のエネルギー保存則は、エネルギー積分と呼ばれるテクニックを用いて、運動方程式と万有引力の法則から導出できる(その詳細は割愛する)。全体を で割っても、保存則が成立するので、軌道力学では通常 を省略した以下の形式を用いる。
ここで、は軌道エネルギーである。詳しい説明は割愛するが、この軌道のエネルギー保存則と角運動量保存則(ケプラーの第2法則:面積速度一定の法則)を用いて式変形を行うことで(参考文献1.参照)、軌道エネルギー と軌道長半径 は反比例の関係にあり、以下のような式が得られる。
軌道周期が1年の共鳴軌道では、探査機の軌道長半径と地球の軌道長半径は一致している。そのため、探査機と地球の軌道のエネルギーは一致するはずである。したがって、探査機の位置、速度 と地球の位置 、速度 の間には、以下の関係が成立する。
なお、各文字の添字は宇宙機(SpaceCraft)の略であり、 は地球の惑星記号である。地球出発時において、探査機の位置と地球の位置は同じであるため、 である。したがって、地球出発時において、「探査機の速度の大きさ」と「地球の速度の大きさ」は一致するはずである。すなわち、
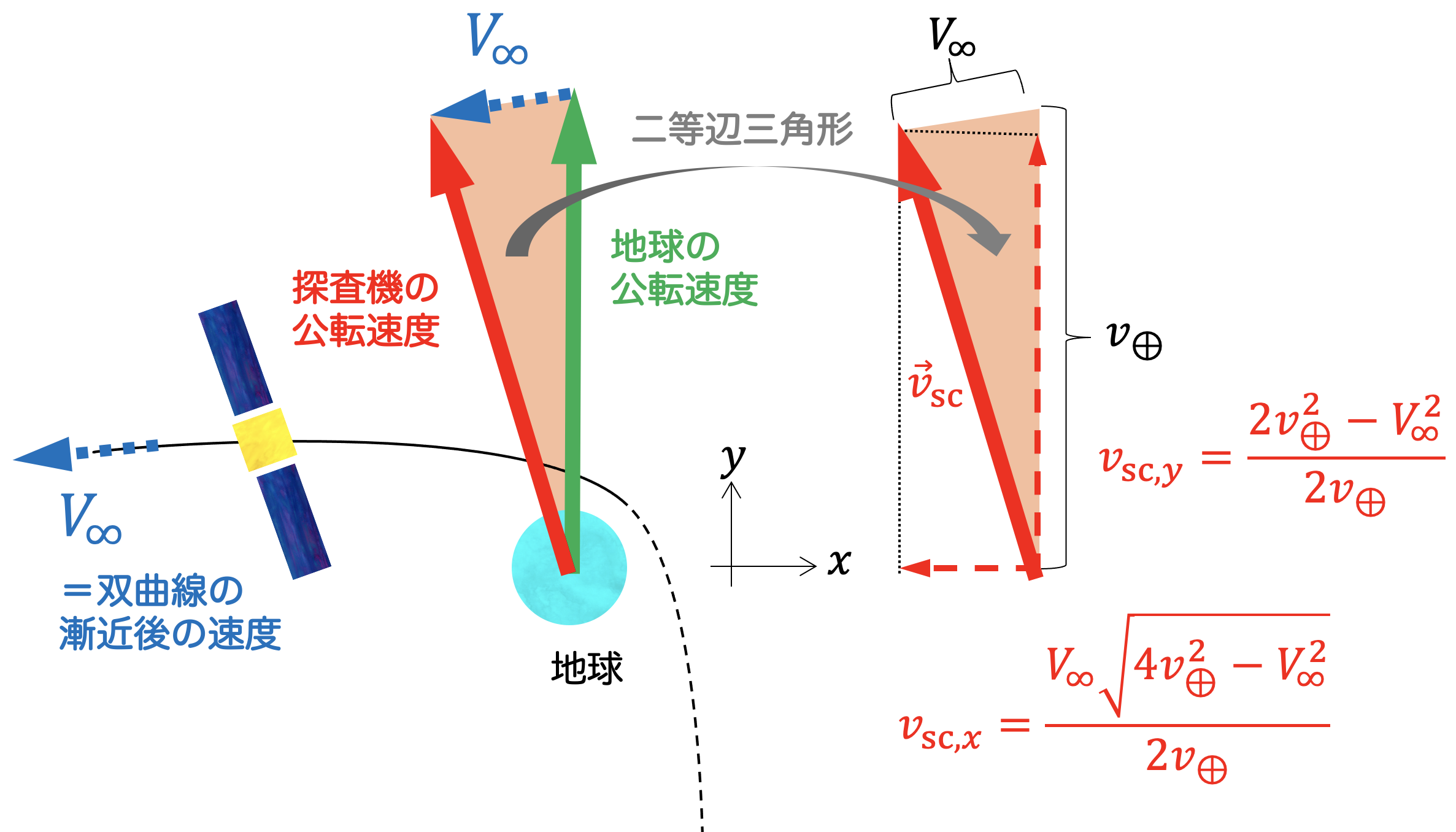
である。一致するのは、あくまでの速度の大きさであり、速度ベクトルの方向は異なっていても構わない。ただし、ロケットの打上げ能力の観点から、ある程度制約されてしまう。探査機の公転速度ベクトルと地球の公転速度ベクトルの差は、 (ブイ・インフィニティ)と呼ばれる。地球から探査機を打ち上げる際の双曲線軌道を考えたとき、この は「地球の重力が作用する領域から十分離れた点での、地球に対する探査機の相対速度」でもある。そのため、大きな を達成するためには、打上げ能力の高いロケットが必要となる。 が与えられると、方向を含めた探査機の速度ベクトル は幾何学的に計算することができる。
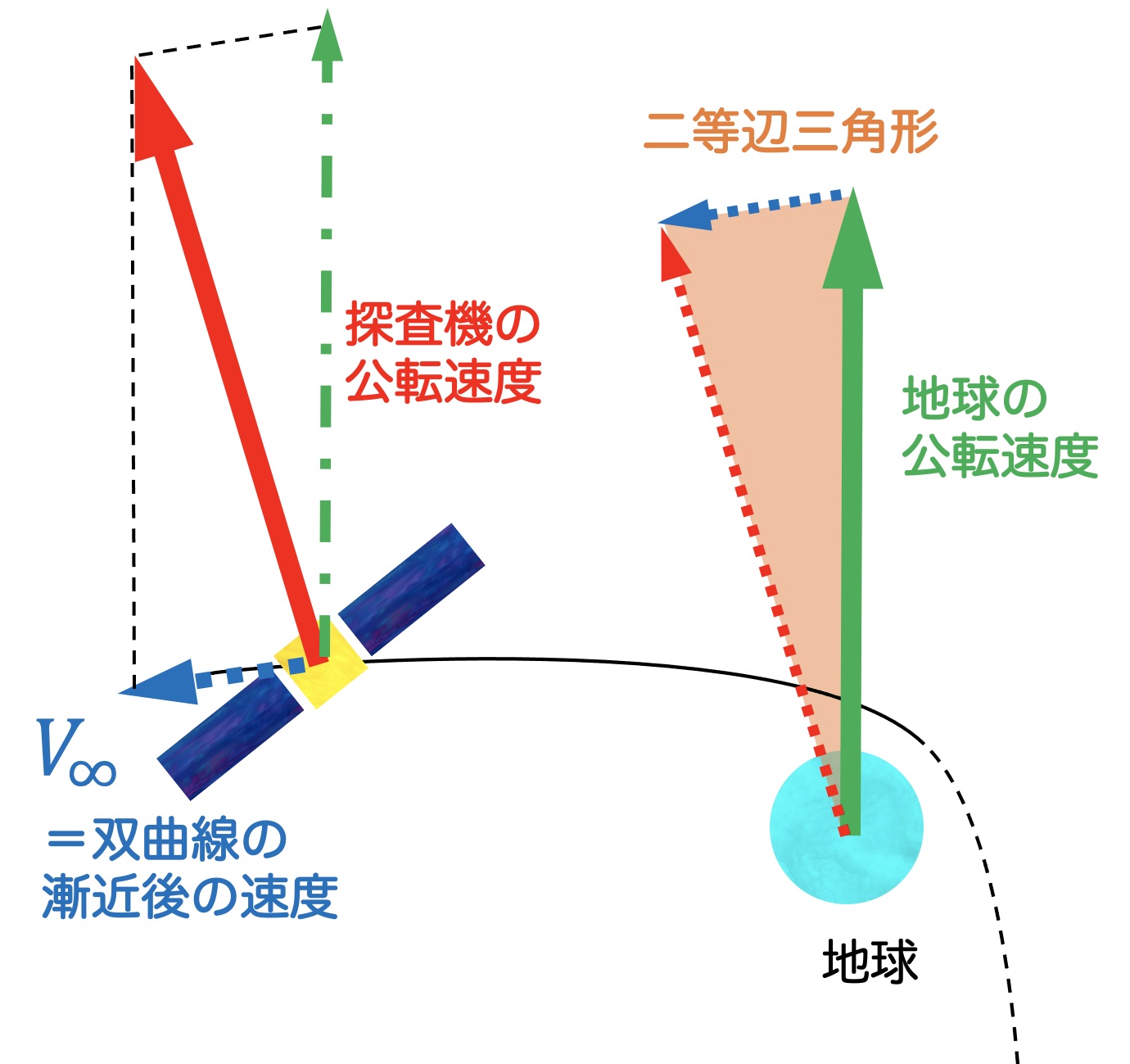
さて、座学が長くなったが、Pythonプログラミングで早速確認してみよう。まずは二体問題を仮定して、速度の大きさが同じ・方向が異なる場合であっても、1年後に同じ位置に戻ってくることを確認しよう。位置の時間変化をmatplotlibで描画してみると、1年後に元の位置に戻ってきていることが確認できる(2つ目のグラフから、1年後に同じ位置に帰ってきていることが読み取れる)。
# Pythonもモジュールを読み込み
import numpy as np # 数値計算ライブラリ
from scipy.integrate import odeint # 常微分方程式を解くライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ
# 二体問題の運動方程式
def func_twobody(x, t):
GM = 1.327e11 # 万有引力定数×中心天体の質量, km^3/s^(-2)
r_norm = np.sqrt(x[0]**2 + x[1]**2)
dxdt = [x[2],
x[3],
-GM*x[0]/(r_norm**3),
-GM*x[1]/(r_norm**3)]
return dxdt
# 条件の設定
r_earth = 149597870.7 # 地球の公転軌道半径, km
v_earth = np.sqrt(1.327e11/r_earth) # 地球の公転速度, km/s
vinf = 5 # 地球公転速度に対する相対速度V∞, km/s
v_sc_x = np.sqrt(4*v_earth**2-vinf**2)*vinf/(2*v_earth) # 探査機の公転速度のx成分, km/s
v_sc_y = (2*v_earth**2 - vinf**2)/(2*v_earth) # 探査機の公転速度のy成分, km/s
x0 = np.array([r_earth, 0.0, -v_sc_x, v_sc_y]) # 位置, 速度, km, km/s
t = np.linspace(0,365*24*60*60,100) # 1年分を100ステップで刻む
# 微分方程式の数値計算
sol = odeint(func_twobody, x0, t)
# 軌道の描画
theta = np.linspace(0,2*np.pi,100)
plt.plot(r_earth*np.cos(theta),r_earth*np.sin(theta),'b', label="Earth") # 地球の軌道
plt.plot(sol[:, 0],sol[:, 1], 'r', label="Spacecraft")
plt.plot(sol[0, 0],sol[0, 1], 'ro', label="Initial Position")
plt.grid() # 格子をつける
plt.legend(loc="lower right")
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.xlabel('x, km')
plt.ylabel('y, km')
plt.show()
# 位置の時間変化の描画
plt.plot(t, sol[:, 0],'m',label="r_x") # 位置ベクトルのx成分の時間変化
plt.plot(t, sol[:, 1],'g',label="r_y") # 位置ベクトルのy成分の時間変化
plt.grid() # 格子をつける
plt.xlabel("Time, s")
plt.ylabel("Position, km")
plt.legend()
plt.show()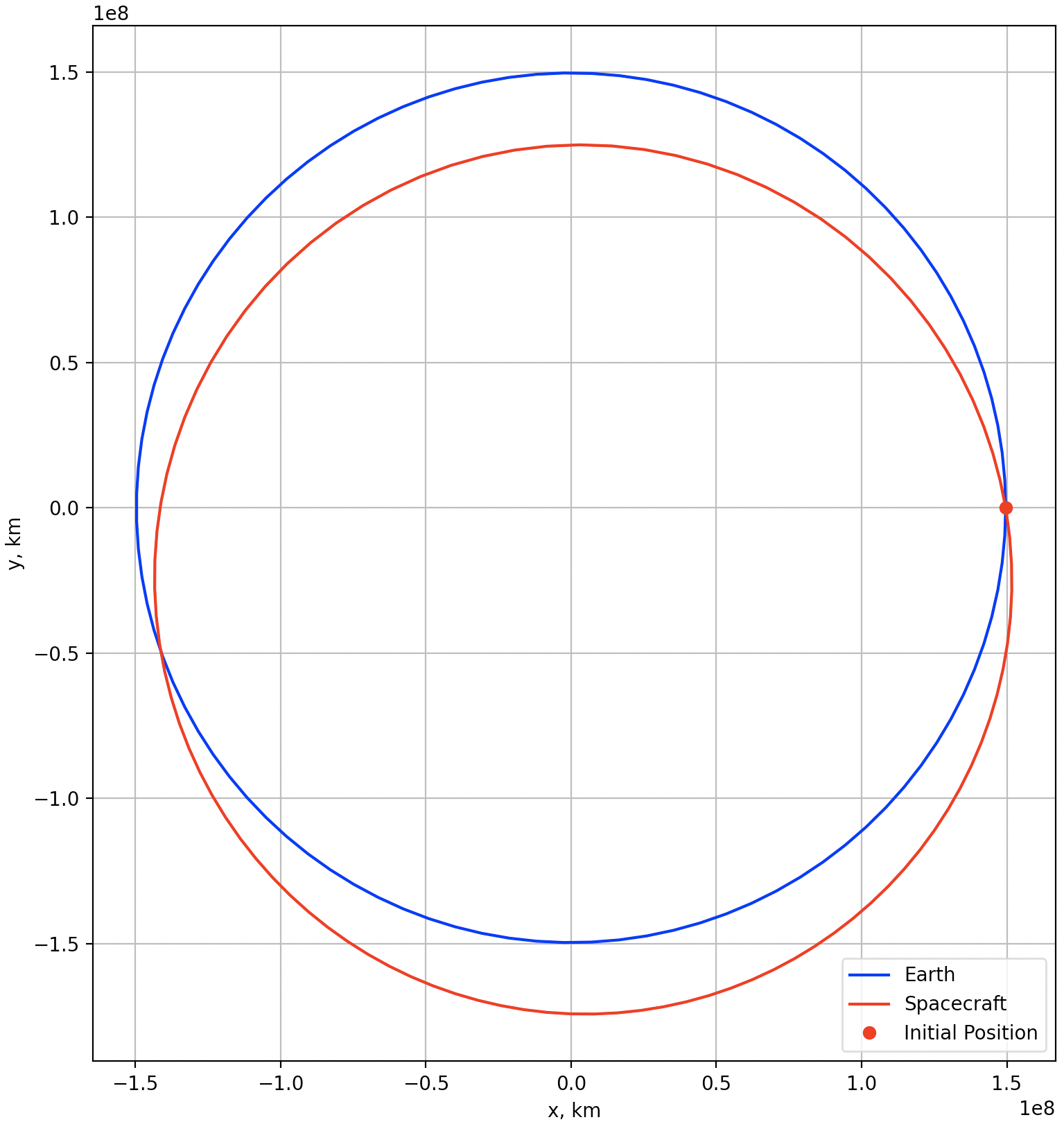
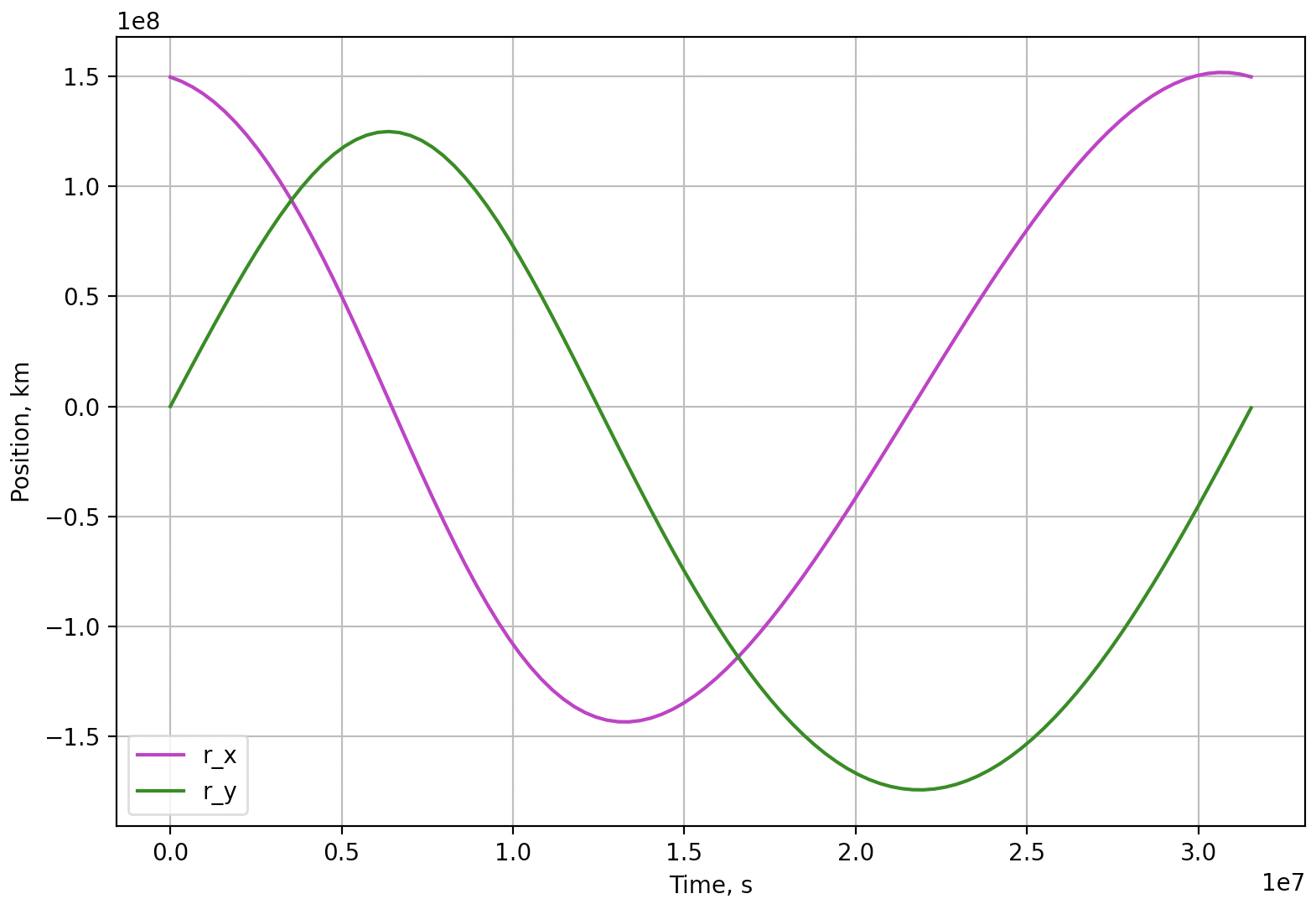
「はやぶさ」の打上げから地球スイングバイに至るまでとほとんど同様の軌道が得られたことが確認できただろうか。さて、このプログラムで用いた「条件の設定」について、少し補足しておく。
r_earthは地球の公転軌道半径であり、1天文単位=149597870.7
kmという値を設定している。
v_earthは地球の公転速度であり、軌道のエネルギー保存則
にを代入すると、
と計算できる。
vinfは前述した(=探査機の公転速度ベクトルと地球の公転速度ベクトルの差)である。ロケットの打上げ能力によって定まる量だが、ここではある程度現実的な値として5km/sという値を設定している。
v_sc_xとv_sc_xは宇宙機の公転速度ベクトルの成分と成分である。
と
が与えられているため、二等辺三角形に関する幾何学的問題を解けば、以下のような関係式が得られる。
地球スイングバイを用いた軌道設計をしてみよう
地球スイングバイを用いた軌道設計を行うための準備が整った!いよいよ、ここからは地球スイングバイを用いた軌道設計をしてみよう。地球出発時の初期条件として、さきほど紹介した1年の共鳴軌道を用いる。この共鳴軌道は二体問題で設計されているため、最初の0.2年間(この0.2年間という数字はテキトーに決めているため、0.1年でも0.9でも良い)は二体問題で軌道伝播を行うことにする。試しにN体問題で軌道伝播する実験も行ってみて欲しいが、探査機の初期位置が地球の位置と一致しているため、重力が無限大に大きくなり、軌道が発散してしまう。
0.2年間二体問題で軌道伝播を行うと、探査機の位置と地球の位置が十分に離れてくる。ここから先は、地球重力も考慮したN体問題で軌道伝播してみよう。そのままN体問題で軌道伝播してみると、地球スイングバイの影響でわずかに軌道が変わっているように見えるが、あまり大きな軌道変化が見られない。そこで、ΔV(デルタ・ブイ)と呼ばれる軌道制御を加えて、良い感じに地球スイングバイができるように、少し調整することを考えてみる。
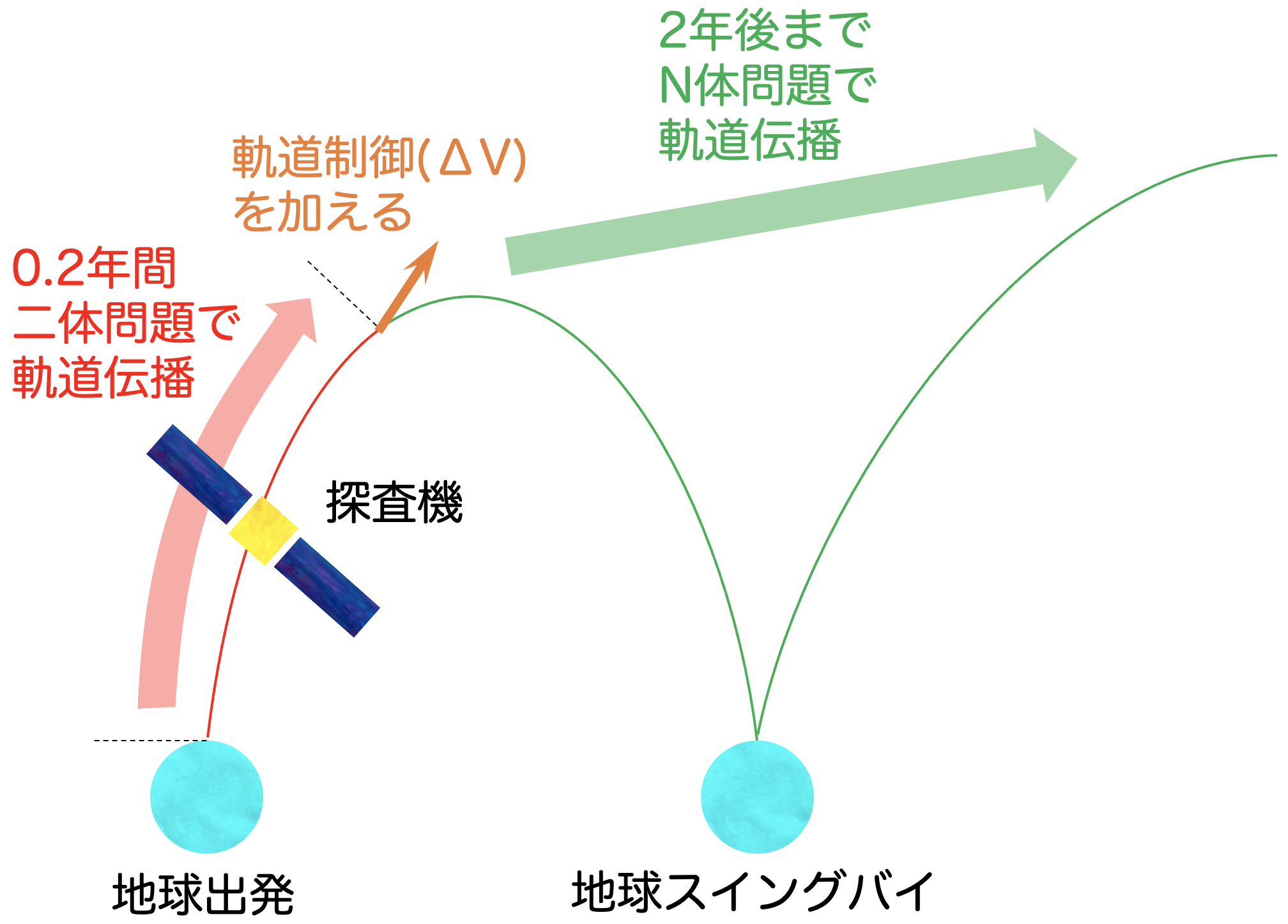
ΔVとは速度(Velocity)の変化量(Δ)で表現される軌道制御量であるが、もう少し解説を加えておく。ある時刻における探査機の位置と速度が与えられると、その後の探査機の軌道が計算できることを、これまで確認してきた。そのため、探査機の軌道を変更(制御)するには、探査機の位置あるいは速度を変更すれば良い。あるタイミングで急に探査機の位置を変更すると、瞬間移動していることになり、物理的にやや不自然である。そこで、軌道設計の分野では、慣例的に、速度を変更することで軌道制御を行う。速度も急に変わると不自然だが、ロケットのような推進機を用いて、軌道力学的なスケールを考えたとき、瞬間的に速度が変化していると考えても差し支えないことが多い。ただし、「イオンエンジン」のような推進機を用いて、ゆっくり軌道制御する場合は、少し話が複雑になる(ので、ここで詳しく説明するのは控える)。
軌道制御を加えるには、軌道伝播を途中で止めて、そこで速度変化(ΔV)を与えると良い。どこで軌道を区切っても良いし、何回区切っても良いが、どこでΔVを与えるかによって軌道変更の効率が変わる。ここでは、一旦、効率は無視して、例えば、軌道が二体問題からN体問題に切り替わる出発から0.2年後のところでΔVを加えてみよう。ΔVの大きさと方向と方向も、軌道変更の効率に大きく寄与する。ここでは、試行錯誤の結果、
方向に0.0055
km/s(=5.5m/s)のΔVを与えてみる。試行錯誤というと高尚なことをしているように思えるかもしれないが、大したことはしておらず「方向に0.002km/sだったら、どういう結果になるか?」「
方向に-0.001km/sだったら、どういう結果になるか?」等を実際にプログラミングを走らせて、軌道を描画しながら、決めるという地味なことを行った。その際に、地球に対する探査機の相対距離をmatplotlibで描画したり、複数のΔV条件の結果をまとめて表示すると便利である。「専門家は、もっと良い方法を使っていないの?」と問われると、答えはYesであり、Noでもある。専門家は詳しくは説明しないが、「軌道最適化」「ランベール問題およびパッチドコニックス」「状態遷移行列(Station
Transition
Matrix)を用いた感度解析」等のテクニックを使って、もっと効率的に軌道設計を行なっている。一方で、こうしたテクニックも万能ではないので、困ったときは、いま紹介したような「とりあえず、いろんな値に設定して、試してみる」というアプローチ(専門的にはグリッドサーチと呼んでいる)を用いることがある。
では、実際にPythonプログラミングを用いながら、地球スイングバイを用いた軌道設計を確認してみよう。
# Pythonもモジュールを読み込み
import numpy as np # 数値計算ライブラリ
from scipy.integrate import odeint # 常微分方程式を解くライブラリ
import matplotlib.pyplot as plt # 描画ライブラリ
# 二体問題の運動方程式
def func_twobody(x, t):
GM = 1.327e11 # 万有引力定数×中心天体の質量, km^3/s^(-2)
r_norm = np.sqrt(x[0]**2 + x[1]**2)
dxdt = [x[2],
x[3],
-GM*x[0]/(r_norm**3),
-GM*x[1]/(r_norm**3)]
return dxdt
# N体問題の運動方程式
def func_nbody(x, t):
# 条件設定
GM = 1.327e11 # 万有引力定数×太陽の質量, km^3/s^(-2)
GM1 = 3.986e5 # 万有引力定数×地球の質量, km^3/s^(-2)
theta1 = 0*(np.pi/180) # 0degと設定, deg -> rad
period1 = 365*24*60*60 # 地球の軌道周期, sec
a1 = 149597870.7 # 地球の軌道長半径, km
# 地球の位置
r1 = np.array([ a1*np.cos(2*np.pi*t/period1 + theta1), a1*np.sin(2*np.pi*t/period1 + theta1) ])
# 運動方程式の計算
d1 = x[0:2] - r1
r_norm = np.sqrt(x[0]**2 + x[1]**2)
d1_norm = np.sqrt(d1[0]**2 + d1[1]**2)
if d1_norm < 6371: # 地球距離が地球半径以下になると衝突してしまうため、エラーを返す
print("ERROR: 地球スイングバイ時の高度がマイナスです!")
dxdt = [x[2],
x[3],
-GM*x[0]/(r_norm**3) - GM1*d1[0]/(d1_norm**3),
-GM*x[1]/(r_norm**3) - GM1*d1[1]/(d1_norm**3)]
return dxdt
# 条件の設定
r_earth = 149597870.7 # 地球の公転軌道半径, km
v_earth = np.sqrt(1.327e11/r_earth) # 地球の公転速度, km/s
vinf = 5 # 地球公転速度に対する相対速度V∞, km/s
v_sc_x = np.sqrt(4*v_earth**2-vinf**2)*vinf/(2*v_earth) # 探査機の公転速度のx成分, km/s
v_sc_y = (2*v_earth**2 - vinf**2)/(2*v_earth) # 探査機の公転速度のy成分, km/s
# 0年〜0.2年の間の軌道伝播(二体問題)
x0 = np.array([r_earth, 0.0, -v_sc_x, v_sc_y]) # 位置, 速度, km, km/s
t_span = np.linspace(0,0.2*365*24*60*60,200) # 0.2年分を200ステップで刻む
sol_0to1 = odeint(func_twobody, x0, t_span)
# 0.2年〜2年の間の軌道伝播(N体問題)
x1 = sol_0to1[-1,:] + [0,0,0.0055,0] # 軌道伝播された位置・速度に軌道制御(ΔV)を加える
t_span1 = np.linspace(0.2*365*24*60*60,2*365*24*60*60,200) # 0.2年〜2年分を200ステップで刻む
sol_1to2 = odeint(func_nbody, x1, t_span1)
# 軌道の描画
theta = np.linspace(0,2*np.pi,100)
plt.plot(r_earth*np.cos(theta),r_earth*np.sin(theta),'b', label="Earth") # 地球の軌道
plt.plot(sol_0to1[:, 0],sol_0to1[:, 1], 'r', label="Spacecraft Before Delta-V")
plt.plot(sol_1to2[:, 0],sol_1to2[:, 1], 'g', label="Spacecraft After Delta-V")
plt.grid() # 格子をつける
plt.legend(loc="lower left")
plt.gca().set_aspect('equal') # グラフのアスペクト比を揃える
plt.xlabel('x, km')
plt.ylabel('y, km')
plt.show()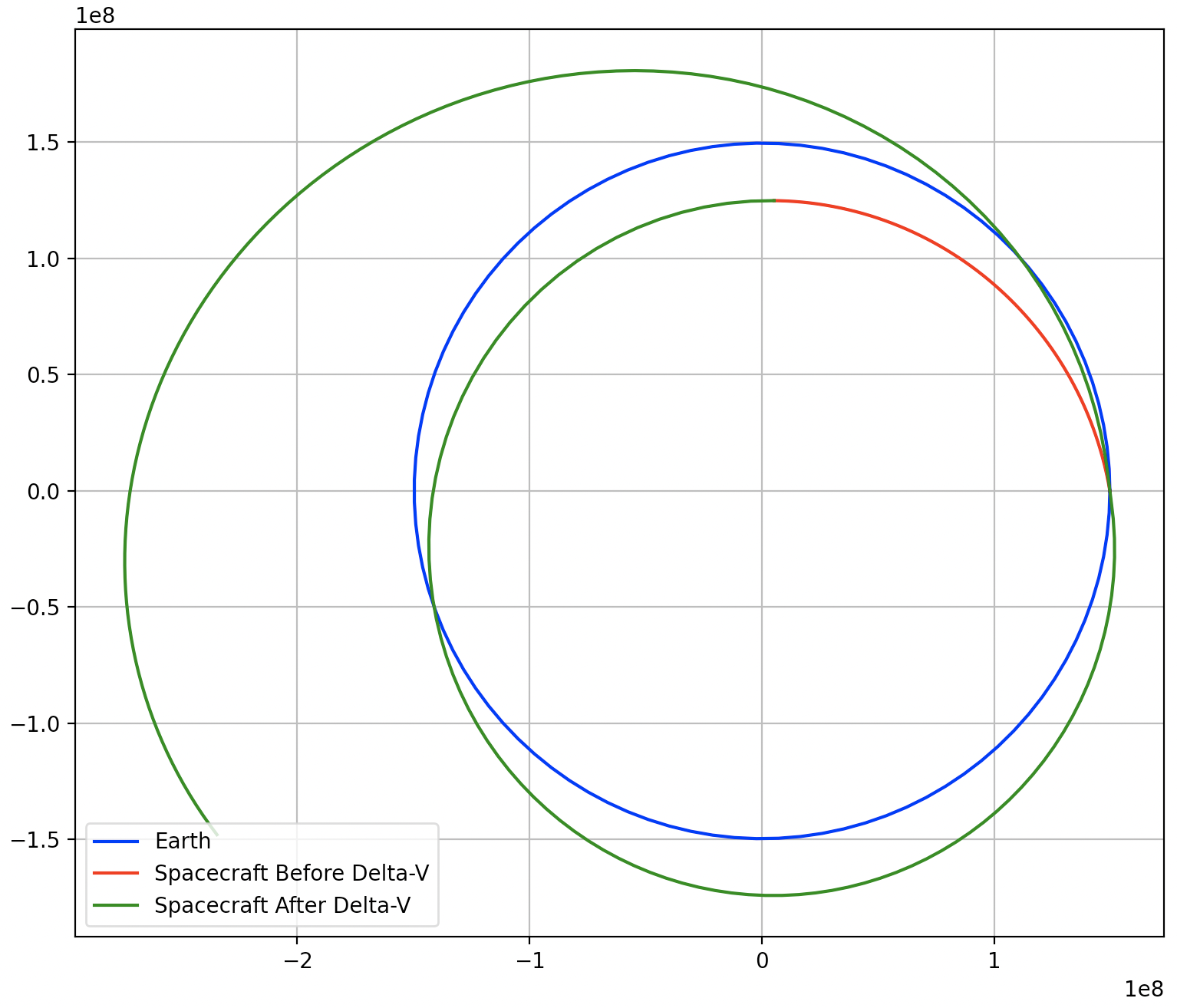
いかがだろうか??地球スイングバイを経由することで、探査機は離れた太陽距離まで飛行することが確認できた。なお、上記のプログラムは、ほとんどがこれまで説明したものの寄せ集めであり、N体問題の軌道伝播の設定でtheta1 = 0*(np.pi/180) # 0degと設定, deg ->
radの部分を変更した以外は、以下とそれに対応する描画を書き加えたくらいである。以下のコードでは、0年〜0.2年の間を二体問題で軌道伝播し、0.2年後の位置・速度に+[0,0,0.0055,0]を加えて、2年後までN体問題で軌道伝播している。
# 0年〜0.2年の間の軌道伝播(二体問題)
x0 = np.array([r_earth, 0.0, -v_sc_x, v_sc_y]) # 位置, 速度, km, km/s
t_span = np.linspace(0,0.2*365*24*60*60,200) # 0.2年分を200ステップで刻む
sol_0to1 = odeint(func_twobody, x0, t_span)
# 0.2年〜2年の間の軌道伝播(N体問題)
x1 = sol_0to1[-1,:] + [0,0,0.0055,0] # 軌道伝播された位置・速度に軌道制御(ΔV)を加える
t_span1 = np.linspace(0.2*365*24*60*60,2*365*24*60*60,200) # 0.2年〜2年分を200ステップで刻む
sol_1to2 = odeint(func_nbody, x1, t_span1)より発展的な内容に興味がある読者は、
- 軌道制御ΔVを変化させて、何が起こるか確認してみよう。少し変化させるだけでも、スイングバイ後の軌道が大きく変わることを確認してみよう。
- 探査機の力学的エネルギーの時間変化をプロットして、地球スイングバイ前後で変わっているか確認してみよう。
- 地球スイングバイ近傍での、地球に対する探査機の軌道を描画してみよう。地球スイングバイは時間スケールとしても短い間に起きる現象なので、200ステップの時間刻み幅ではなく、もっと細かい幅で表示する必要がある。うまく行っていれば、双曲線軌道になっているはずである。「地球が双曲線の焦点にあるか?」「V∞の大きさはどうなっているか?」等を確認してみよう。
スイングバイを用いて様々な軌道設計問題を解いてみよう
本記事の最後に、読者が様々な軌道設計問題を解いてみるためのヒントを与えたいと思う。
軌道制御量(ΔV)の与え方を工夫してみる
今回扱った問題は0.2年後に方向に0.0055km/sのΔVを与えた。そして、それは試行錯誤の結果決めたと言ったが、少しウソをついた。いくつか専門家としての直感をもとに決めている。
- 0.2年後にした理由は、その頃、探査機が近日点(=探査機が太陽に最も近づく点)近傍を通過するからである。多くの場合、近日点あるいは遠日点(=探査機が太陽から最も遠ざかる点)近傍でΔVを与えると効率的である。
- 方向ではなく、 方向を選んだのには訳がある。多くの場合、速度方向(あるいは速度と逆行する方向)に対してΔVを与えると効率的である。
この直感は万能ではないことを心に留めておいていただきたいが、試行錯誤の過程で、このような”経験則”を獲得し、その経験則を用いることで、試行錯誤にかける労力を削減することができる。
金星・火星・木星スイングバイを考えてみる
今回は地球スイングバイのみを考えたが、地球スイングバイの先に金星・火星・木星等の複数の天体をスイングバイをする軌道設計を考えてみてもらいたい。ちょうど良いタイミングに、ちょうど良い場所に惑星がないと、他の惑星のスイングバイはうまく行かない。なので、複数の惑星をスイングバイする軌道設計では「いつであれば、その軌道が成立するのか?」が非常に重要である。今回は、N体問題の軌道伝播で を自由に選べるので、ちょうど良いタイミングに、ちょうど良い場所に惑星がくるように を選んでもらえれば良い。
グリッドサーチ以外のアプローチを考えてみる
今回は、ΔVを1回与えて、1回地球スイングバイする問題を考えた。金星・火星・木星等の複数の天体をスイングバイするような問題を考えるときには、複数の場所で軌道を区切って、複数の場所でΔVを与えても良い(むしろその方が軌道設計がやりやすくなるだろう)。スイングバイすべき天体の数が増えれば増えるほど、グリッドサーチで探すべき変数が増え、限界を感じるだろう。では、グリッドサーチ以外に良い方法はないのか?そういう方法を考える研究が”軌道設計の研究”である。この記事を、ここまで読み進められた読者は”軌道設計の研究”の入り口に立っている。答えは1つではないし、専門家の間でも万能な方法は見つけられていない。ノートPCが1台あれば研究できるような分野でもあるので、ここまでの話で興味が湧いてきた読者には、是非研究してもらいたいと思う。
おわりに
さて、本記事の目標は、「Lv. 5であってもスイングバイを用いた軌道設計ができるようにある」ことだったが、スイングバイを用いた軌道設計ができるようになっただろうか?また、同時に本格的なスイングバイ軌道設計には、Lv. 50以上必要であるという奥深さも感じ取れただろうか?我々専門家は、今回紹介できなかった様々なテクニック(例えば、参考文献2を参照)を用いて、スイングバイ軌道を設計している。多くの教科書では、まず二体問題に関する軌道力学の諸々の知識を説明した上で、パッチドコニックス(Patched Conics)という二体問題を拡張するアプローチでスイングバイが説明される。今回の記事では、あえて教科書的ではないアプローチで説明をした。初めての試みなので、分かりづらさ・間違いに気づいた読者は、個人的に連絡いただきたい。今回のような「専門家がよく用いるアプローチ」ではないやり方を通じて、柔軟な考え方をもった読者に、何か面白い軌道設計手法が発案されることを期待している。
参考文献
- “Vis-viva Equation(軌道力学におけるエネルギー保存則)"、https://en.wikipedia.org/wiki/Vis-viva_equation、アクセス日:2022年7月30日
- 尾崎直哉、”小天体マルチフライバイを実現するための『小天体フライバイサイクラー軌道』〜機械学習による軌道設計とその展望〜”、あいさすGATE、2022年07月21日、(https://www.isas.jaxa.jp/home/research-portal/gateway/2022/0721/、アクセス日:2022年7月30日)
著者情報

尾崎 直哉(Naoya OZAKI)
JAXA宇宙科学研究所
テニュアトラック特任助教・宇宙ミッションデザイナー・博士(工学、東京大学、2018年)。世界初の超小型深宇宙探査機PROCYON(プロキオン)の開発を中心に、多くの深宇宙探査ミッションに携わる。ESA・NASA・JAXAの3機関にて修行を積んだ軌道設計のスペシャリスト。